Как Декарт победил Матрицу – Православный журнал «Фома»
Приблизительное время чтения: 5 мин.
Вы – рабы. Рабы инстинктов и рефлексов, электрических процессов своего мозга, химических процессов своего организма. Как заложники компьютерной иллюзии из фильма «Матрица» вы не управляете собой. Это вами управляют.
Именно такой вывод можно сделать (и многие его делают!), когда читаешь статьи о последних научных открытиях в области изучения человеческого мозга, эволюционной психологии и пр. Но неужели правда, что вся наша свобода – просто иллюзия, а люди – только пешки в непознаваемой игре природы?
На этот вопрос в проекте Академия «Фомы» отвечает Александр Доброхотов, доктор философских наук, ординарный профессор Высшей школы экономики.
Вопрос о свободе — вечная философская проблема — сегодня снова широко обсуждается в связи с рядом новых научных открытий.
Когда возникает иллюзия? Когда есть некоторое начальное представление о предмете — и последующая интерпретация, которая опровергает то, что нам казалось истинным изначально. Например, я вижу, что рельсы у горизонта сходятся в одну линию. Это мое первое представление. Однако ученый тут же объяснит мне, что оно неверно, что это всего лишь оптическая иллюзия, и рельсы на самом деле параллельны.
Мы видим, что палка в воде кажется сломанной, что Солнце вращается вокруг Земли, но наука разоблачает эти иллюзии.
Однако именно здесь-то и нужно осознать то, что поняли философы: существуют такие основоположения, которые просто не могут быть иллюзорными. В них нет этой двойственности, нет второго, скрытого от нас плана.
Так Рене Декарт (знаменитый французский философ XVII века), в поисках такого изначального и предельного основоположения вывел свое знаменитое: «мыслю, следовательно существую» (когито эрго сум).
Ведь не может быть ложным тот факт, что я мыслю. Для того чтобы сделать такую мысль ложной, ее уже нужно помыслить.
И даже если я стану отрицать свободу, в самом факте такого отрицания осуществится свободный акт.
«Ты веришь в судьбу, Нео?»
В том же ключе рассуждал и блаженный Августин («О Граде Божьем», кн. XI, 26), который, отвечая скептикам, подвергающим всё — и даже человеческое познание — сомнению, указывал, что в самом акте сомнения содержится положительное, истинное высказывание. Я уверен в том, что сомневаюсь. Декларируя сомнение, я делаю это без сомнения. Я утверждаю это. Так само сомнение для Августина и Декарта доказывает что, человек способен мыслить положительно, плодотворно, и этого у него не отнимешь.
Но Декарт идет дальше и вводит последнее, предельное допущение.
При этом осознание самого себя в принципе не может быть иллюзорным. Почему?
Да потому что тогда демон должен был бы «инсталлировать» в нас эту иллюзию, то есть наше сознание должно было бы быть некой доступной для вторжения идеальной машиной, производящей цепочку ментальных операций. Но сама возможность духовной беззащитности человека перед манипуляциями превосходящих его сознание сил привела Декарта в состояние религиозного ужаса. Ведь выражение «злой демон» является лишь псевдонимом гипотезы «злого Бога», которая изображает мир как тотальную власть злого сверхразума. В самом деле, а что если Бог – злой? Это же предельный ужас!
Разгадку мы уже знаем: само сомнение – несомненно – доказывает бытие самосознания.
Самосознание абсолютно бессодержательно, и именно его пустота – защита от возможной фальсификации, подделки: содержания просто нет, а есть только ничем не обусловленное бытие. То есть
Но злой демон, который так страшил Декарта, был не просто абстрактной моделью. Декарт находился в начале того процесса, который сегодня, кажется, все-таки выдохся: превращения мира в исчисляемую предметность, полностью контролируемую научным рассудком. И именно Декарт открыл предел внушаемости, за который не перейти ни демону (потому что он не сможет), ни Богу (потому что Он не хочет). Сознание не имеет предметного содержания, поэтому никакое содержание не может быть в него вложено, как программа в компьютер.
Но даже если мы допустим ситуацию прямого «инсталлирования» туда какой-либо информации, сам акт самосознания или присвоит
Другими словами, демон может внушить все, кроме самосознания.
Gabriel Kronisch
Отсюда, кстати, вытекает и другое следствие: непрозрачность для нас чужого «я». Наша мысль, направленная на чужое «я», схватывает лишь внешние его проявления.
И это чрезвычайно важно: именно благодаря такой непрозрачности возможно настоящее общение, когда личности свободно открывают себя друг другу и нет необходимости превращать другого в «вещь», чтобы понять его.
Итак, никакие биологические процессы или социальные условия не могут определить или ограничить нашу свободу. Потому что человеческая свобода сама себя порождает и обосновывает. Она в принципе не может быть иллюзорной.
Здесь уместно вспомнить великого детерминиста Спинозу. Он утверждал: если бы летящий камень думал, он мог бы подумать, что летит свободно, тогда как на самом деле он летит детерминировано, по закону природы. И в этом резкое отличие Спинозы от Декарта, который сказал бы: если камень действительно подумал, что он свободен – он стал свободен.
via GIPHY
Ведь свобода существует именно как действие, как поступок. Ее «исполняют». Никакие заданные условия не отменяют того, что я определяю себя, и я становлюсь таким в результате моего свободного выбора.
Сейчас эти споры обострились, особенно в связи с современной философией сознания, многие сторонники которой полагают, что если в самом «механизме» психики мы найдем детерминацию, это может вообще отменить свободу.
Но в том-то и дело, что свободу отменить нельзя. Ей не нужны посредники во внешнем мире. Она рождается в тот момент, когда я говорю себе: я свободен.
Читайте также:Христианство сделало человека личностью
На заставке фрагмент фото: marcoverch
Картезианское сомнение Декарта: отражение идей философа в фильме «Матрица»: rabota_psy — LiveJournal
Люди погружены в желеобразную субстанцию. Их жизнь поддерживается многочисленными трубками и проводами, которые влияют на мозг, создавая иллюзию полноценной жизни.
Это фрагмент фильма «Матрица», изображающий 2197 год. Человечество попало под власть машин. Тепло и электрическая активность человеческих тел используются искусственным интеллектом как источник энергии.Планета окутана мраком, города разрушены. Люди, порабощенные машинами, не знают об этом. Они живут в мире иллюзий, им кажется, что жизнь течет как обычно. Нео — один из них. Благодаря красной капсуле он узнает правду и начинает борьбу с суперкомпьютером.
Портрет Декарта кисти Франса Халса (1648)
Могла ли такая ситуация возникнуть на самом деле? Об этом еще в XVII веке задумался математик и философ Рене Декарт.
Картезианское сомненье
Возможно запереть человека в рамках сна, содержание которого определяется кем-то, создать условия, в которых индивид не будет осознавать, что воспринимаемая им реальность совсем не реальна. Чтобы поверить в это, нужно обладать скептицизмом. Именно это качество было присуще Декарту.
Диспут Декарта (справа) и королевы Кристины, картина Пьера-Луи Дюмениля
Скептиком называют человека, сомневающегося во всем.
Рене Декарт — король скептиков. Ученый разработал форму скептицизма, названную картезианским сомненьем. Он предположил, что все его убеждения ложны, поэтому их надо проверить.
Как Декарт перепроверил свои убеждения
Он решил действовать кардинально, проведя аналогию с корзиной фруктов. Чтобы отделить гниль от хороших плодов, следует все содержимое высыпать, а затем положить в нее лишь уцелевшие экземпляры. Проверку ученый начал с эмпирических убеждений, то есть тех, которые подтверждаются органами чувств.
Декарт пришел к выводу, что слух, зрение, обоняние, осязание не могут гарантировать верность убеждений. Философ привел множество примеров, доказывающих этот факт. Когда человек болен, еда кажется горькой. Руки после игры в снежки ощущают воду комнатной температуры как горячую.
Декарт продолжил рассуждения. В таком случае способен ли спящий осознать ирреальность сновидений? Да, как только индивид просыпается, он понимает, что это был всего лишь сон. Такое сомнение, которое можно развеять, сверившись с собой, он назвал локальным.
Глобальное сомнение
Затем ученый предположил, что вся окружающая реальность ложная. Все вокруг не такое, каким воспринимается (как в «Матрице»). Сомнение, при котором человек не может выйти за его границы и перепроверить, было названо глобальным. Декарт выдвинул гипотезу о существовании злобного гения, который мог создать иллюзорный мир и запереть в нем людей. Философ понимал невероятность наличия такого существа, но он не мог обнаружить и доказательств его отсутствия.
Отчаявшийся ученый все-таки нашел выход. Он понял, что может сомневаться во всем кроме того, что сомневается, то есть мыслит. А если есть мысль, то существует и реальный мыслитель. Так родилась знаменитая декартовская фраза: «Я мыслю, следовательно, существую».
Текст полностью:
https://zen.yandex.ru/media/philosophy/kartezianskoe-somnenie-dekarta-otrajenie-idei-filosofa-v-filme-matrica—5adafaadbcf1bccf58fb4d97
РЕНЕ ДЕКАРТ И ЗЛОЙ ДЕМОН. «Матрица» как философия
КАК МЫ МОЖЕМ ОКАЗАТЬСЯ В МАТРИЦЕ: РЕНЕ ДЕКАРТ И ЗЛОЙ ДЕМОН
Гипотеза, гласящая, что мир, который мы видим, слышим и осязаем, может оказаться иллюзией, развивается сторонниками философского направления под названием скептицизм.
Скептики утверждают, что мы не можем с уверенностью утверждать, существует ли внешний мир. Подобно героям «Матрицы», замечающим в привычном мире подозрительные вещи, они отстаивают мнение, что наши знания о мире могут быть поставлены под сомнение.
Гипотезы скептицизма особенно популярны у двух групп людей. Первая — это молодые люди, чей подростковый бунт против простых истин, навязываемых родителями, иногда принимает метафизическую форму, толкая их на заявления вроде «Ничто не является тем, чем кажется!» или «Только я знаю, какова реальность на самом деле!».
Вторая и более важная группа — это философы, которые, в свою очередь, тоже делятся на две группы. К первой группе относятся философы, еще не переросшие стадию «метафизического бунта» и поэтому находящие изучение абсурдных и заведомо ложных гипотез увлекательным и приятным занятием. Философы этой группы могут даже открыто признавать лозунги молодых скептиков вполне убедительными. Для нас же сейчас важна вторая группа философов.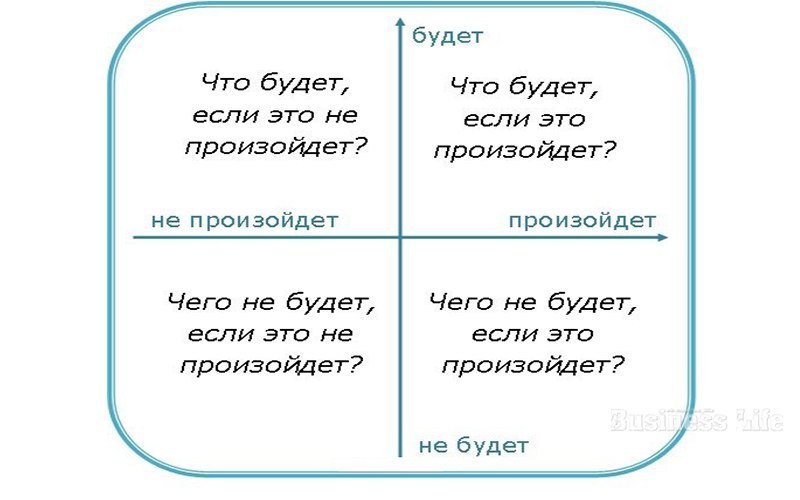
В классическом труде «Размышления о первой философии» Декарт излагает наиболее существенные аргументы скептицизма, которые должны создать для науки прочную базу. Декарт начинает «Размышления» объявлением о намерении считать недействительными все мнения, которые он сможет поставить под сомнение. Абсолютно верными могут считаться только те мнения, которые пройдут проверку Декарта, и только эти взгляды могут служить надежным научным фундаментом. Радикальное сомнение Декарта является методологическим, то есть оно предназначено служить интеллектуальным целям. Вряд ли Декарт действительно стал бы отрицать все взгляды, которые подвергал проверке; их «недействительность» была лишь временной, эвристическим приемом.
Первыми объявляются недействительными те мнения, которые Декарт считает основанными на чувственном восприятии.
Мы часто подкрепляем свое мнение информацией, полученной посредством зрения, слуха, обоняния и вкуса. Например, мы убеждены, что наш сосед по комнате Йон вернулся с занятий, если видим, как он приближается к дому, и если слышим, как он возится с дверью, то верим, что он снова не может отпереть замок. Однако Декарт отмечает: «Я иногда замечал, что они [чувства] нас обманывают». Это особенно верно в отношении очень маленьких или очень удаленных объектов. Фигура, которую мы принимаем за Йона, может оказаться вором; копошение у дверей может оказаться попыткой вора взломать замок. Из-за того что чувства иногда нас подводят, многие наши суждения, подкрепляемые свидетельством чувств, не удовлетворяют высоким стандартам Декарта, вследствие чего он их отбрасывает.
Продолжая эксперимент, Декарт указывает, что даже такие относительно неоспоримые суждения, как, например, то, что вы сидите в кресле и читаете эту книгу, могут быть подвергнуты сомнению. Конечно, эти суждения кажутся более надежными, чем ваши догадки о Йоне и о том, что он делает на крыльце.
Однако Декарт подчеркивает, что мы часто заблуждаемся в отношении именно таких вещей во сне. Во сне вы можете видеть, что сидите на стуле и читаете эту книгу, хотя на самом деле вы лежите в кровати и у вас быстрая фаза сна. Мы не можем отличить опыт бодрствования от опыта, который мы якобы переживаем во сне, пока не проснемся, Морфеус поддерживает это мнение:
Ты когда-нибудь видел такой сон, Нео, когда был уверен, что это не сон? Что, если ты бы не мог очнуться от этого сна? Как бы ты узнал разницу между миром твоего сна и реальным миром?
На основе своего «сонного» аргумента Декарт делает вывод, что чувственный опыт — не самый надежный механизм проверки, поэтому он отбрасывает все убеждения, сформированные на основе чувственного опыта.
Затем Декарт продолжает наступление на привычные взгляды. Давая нам повод усомниться в представлениях о физическом мире, «сонный» аргумент, кажется, должен оставлять нетронутыми, например, представления о геометрических фигурах.
Как пишет Декарт, «ибо сплю ли я или бодрствую, два плюс три дают пять, а квадрат не может иметь более четырех сторон». Однако Декарт заканчивает свое первое «Размышление» рассмотрением следующего, еще более радикального мысленного эксперимента. Он предполагает, что «не всеблагой Бог, источник истины, но какой-то злокозненный гений, очень могущественный и склонный к обману, приложил всю свою изобретательность к тому, чтобы ввести меня в заблуждение».[28] Такое существо, по словам Декарта, могло бы легко изменить наше мнение о сумме двух и трех или о числе сторон квадрата. Еще проще этому злому демону было бы заставить нас думать, что существует внешний для нас физический мир, в то время как на самом деле «я буду мнить небо, воздух, землю, цвета, очертания, звуки и все вообще внешние вещи всего лишь пригрезившимися мне ловушками, расставленными моей доверчивости усилиями этого гения». Отсюда Декарт делает вывод: «…я буду рассматривать себя как существо, лишенное рук, глаз, плоти и крови, каких-либо чувств».
Прочитав первое «Размышление» Декарта, сложно представить доказательства того, что наша жизнь не является грандиозным обманом, сотворенным злым демоном. Как же мы можем оспорить скептические аргументы, выдвинутые Декартом?
Те, кто видел «Матрицу», могут задать себе еще один вопрос: можем ли мы исключать возможность того, что наши жизни, кажущиеся исполненными смысла, на самом деле лишь иллюзии, созданные в наших мозгах умными компьютерами?
Картезианское сомнение Декарта: отражение идей философа в фильме «Матрица» | „ΦΙΛΟΣΟΦΊΑ“ — ЭНЦИКЛОПЕДИЯ ДЛЯ ЛЮБОПЫТСТВУЮЩИХ
Люди погружены в желеобразную субстанцию. Их жизнь поддерживается многочисленными трубками и проводами, которые влияют на мозг, создавая иллюзию полноценной жизни. Это фрагмент фильма «Матрица», изображающий 2197 год. Человечество попало под власть машин.
Тепло и электрическая активность человеческих тел используются искусственным интеллектом как источник энергии.
Планета окутана мраком, города разрушены. Люди, порабощенные машинами, не знают об этом. Они живут в мире иллюзий, им кажется, что жизнь течет как обычно. Нео — один из них. Благодаря красной капсуле он узнает правду и начинает борьбу с суперкомпьютером.
Портрет Декарта кисти Франса Халса (1648)Портрет Декарта кисти Франса Халса (1648)
Могла ли такая ситуация возникнуть на самом деле? Об этом еще в XVII веке задумался математик и философ Рене Декарт.
Картезианское сомненье
Возможно запереть человека в рамках сна, содержание которого определяется кем-то, создать условия, в которых индивид не будет осознавать, что воспринимаемая им реальность совсем не реальна. Чтобы поверить в это, нужно обладать скептицизмом. Именно это качество было присуще Декарту.
Диспут Декарта (справа) и королевы Кристины, картина Пьера-Луи ДюмениляДиспут Декарта (справа) и королевы Кристины, картина Пьера-Луи Дюмениля
Скептиком называют человека, сомневающегося во всем.
Рене Декарт — король скептиков. Ученый разработал форму скептицизма, названную картезианским сомненьем. Он предположил, что все его убеждения ложны, поэтому их надо проверить.
Как Декарт перепроверил свои убеждения
Он решил действовать кардинально, проведя аналогию с корзиной фруктов. Чтобы отделить гниль от хороших плодов, следует все содержимое высыпать, а затем положить в нее лишь уцелевшие экземпляры. Проверку ученый начал с эмпирических убеждений, то есть тех, которые подтверждаются органами чувств.
Декарт пришел к выводу, что слух, зрение, обоняние, осязание не могут гарантировать верность убеждений. Философ привел множество примеров, доказывающих этот факт. Когда человек болен, еда кажется горькой. Руки после игры в снежки ощущают воду комнатной температуры как горячую.
Декарт продолжил рассуждения. В таком случае способен ли спящий осознать ирреальность сновидений? Да, как только индивид просыпается, он понимает, что это был всего лишь сон.
Такое сомнение, которое можно развеять, сверившись с собой, он назвал локальным.
Глобальное сомнение
Затем ученый предположил, что вся окружающая реальность ложная. Все вокруг не такое, каким воспринимается (как в «Матрице»). Сомнение, при котором человек не может выйти за его границы и перепроверить, было названо глобальным. Декарт выдвинул гипотезу о существовании злобного гения, который мог создать иллюзорный мир и запереть в нем людей. Философ понимал невероятность наличия такого существа, но он не мог обнаружить и доказательств его отсутствия.
Отчаявшийся ученый все-таки нашел выход. Он понял, что может сомневаться во всем кроме того, что сомневается, то есть мыслит. А если есть мысль, то существует и реальный мыслитель. Так родилась знаменитая декартовская фраза: «Я мыслю, следовательно, существую».
- Интересно? Ставьте лайк и подписывайтесь на канал ΦΙΛΟΣΟΦΊΑ.
Ещё нас можно читать во ВКонтакте! - E-mail для связи с редакцией: [email protected]
- Литература: wikipedia.org // kinopoisk.ru // CrashCourse
Ещё нас можно читать во ВКонтакте!Квадрат Декарта — техника принятия решения: 21 апреля 2016, 08:31
Решить, что купить — джинсы или сковородку иногда так же сложно, как принять решение об открытии нового направления в бизнесе. И магический шар предсказаний с ответами «да» или «нет» не поможет, ведь он бесчувственный и не знает предыстории. А вот квадрат Декарта — более практичный инструмент. Что это такое, и как ним пользуются в коворкинге MULTISPACE, мы вам сейчас расскажем.
Что такое квадрат Декарта?
Методика Декарта предлагает найти решение, проанализировав ситуацию сразу с четырех сторон. Чтобы использовать квадрат Декарта, запаситесь 15 минутами, листом бумаги и ручкой. Составьте на бумаге матрицу из четырех квадратов (два на два), в каждом из которых впишите следующие вопросы:
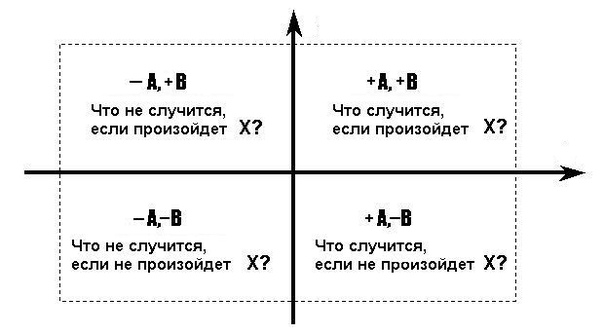
1.
Что случится, если это произойдет?
2. Что случится, если это не произойдет?
3. Что не случится, если это произойдет?
4. Что не случится, если это не произойдет?
Как пользоваться квадратом Декарта?
Начинайте по очереди давать ответы на каждый из приведенных вопросов, в ключе анализа вашей ситуации. Старайтесь дать как можно больше вариантов. Это может открыть новые стороны, о которых вы даже не задумывались.
Отвечая на первые два вопроса (Что случится, если это произойдет? Что случится, если это не произойдет?), старайтесь перечислить плюсы, которые вы получаете в том или ином случае.
Когда будете писать ответы на вопросы, что не случится, то старайтесь продумать минусы от получения или неполучения желаемого.
Давайте рассмотрим пример: вы стоите перед выбором смены сферы деятельности.
Фиксируем плюсы от получения желаемого
Вопрос 1. Что случится, если это произойдет?
Вы попробуете себя в новом направлении, возможно, добьетесь большего успеха, чем у вас есть сегодня, расширите круг знакомств…
Фиксируем плюсы от неполучения желаемого
Вопрос 2. Что случится, если это не произойдет?
Не возникнет необходимости переучиваться и пропадать на работе допоздна, не возникнет риска ухудшения отношений с партнером, не будет дискомфорта от отсутствия знаний…
Пишем минусы от получения желаемого
Вопрос 3. Что не случится, если это произойдет?
Не получите годовой бонус на сегодняшней работе, придется отложить запланированную поездку в отпуск, прервутся со временем отношения с сегодняшними коллегами…
Пишем минусы от неполучения желаемого
Вопрос 4. Что не случится, если это не произойдет?
Не почувствуете себя снова в начале пути, не будет нового витка в работе …
Почему работает квадрат Декарта?
Прежде всего, потому, что мы меняем подход в принятии решения.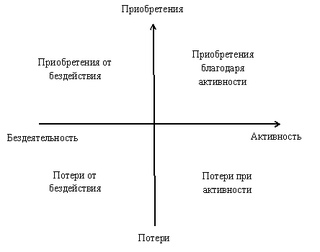
Обычно мы оцениваем сложившуюся ситуацию только с одной точки зрения. И зачастую, это: «что будет, если это произойдет?». Матрица Декарта позволяет отойти от привычного подхода и посмотреть на обстоятельства с 4-х разных сторон. Как результат – у вас на руках взвешенный и продуманный выбор.
Как работает вопросная матрица для анализа трудных ситуаций | Саморазвитие
Чтобы помочь людям в решении возникающих психологических проблем, специалисты используют различные вопросные техники. Одна из самых популярных – так называемый «квадрат Декарта».
Квадрат Декарта
«Квадрат Декарта» используется при принятии трудных решений для анализа альтернатив и выбора лучшей из них. Чтобы определиться с выбором, достаточно ответить на четыре вопроса:
- Что будет, если это произойдет?
- Что НЕ случится, если это произойдет?
- Что будет, если это НЕ произойдет?
- Что НЕ случится, если это НЕ произойдет?
Однако прежде чем принимать наилучшее решение, необходимо как следует проанализировать сложившуюся ситуацию.
Мозг устроен таким образом, что когда мы переживаем сильные эмоции, наши интеллектуальные функции тормозятся. Когда мы сильно расстроены, подавлены или озабочены возникшей проблемой, то нам трудно учесть все обстоятельства ее возникновения, трудно разобраться в себе.
Первый вопрос
Самый первый вопрос, который необходимо задать самому себе в сложной ситуации: «Что именно произошло?». Важно признать то, что случилось, и как-то обозначить/назвать состоявшееся. Например, меня уволили с работы, из-за того, что я плохой работник. При этом важно, чтобы формулировка отражала объективное положение дел и была бы эмоционально нейтральной.
Приведенный выше пример лучше переформулировать так: «Я остался без работы. Увольнение произошло по инициативе руководства; при увольнении использовалась следующая формулировка: …». Понятно, что сам факт увольнения от такой переформулировки слаще не станет, но важно найти такие слова, которые помогут вам успокоиться, снизить негативные эмоции (обиду, злость, печаль) и начать думать над ситуацией более хладнокровно.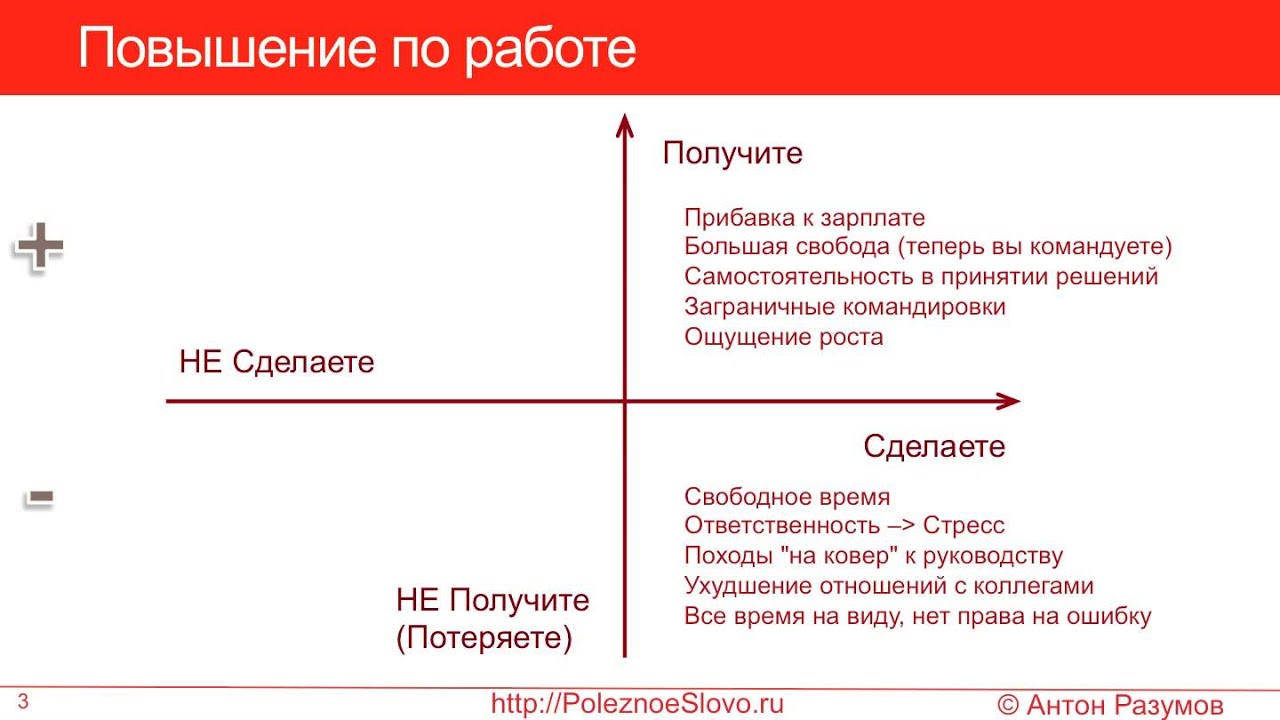
Вопросная матрица
Чтобы окончательно разложить сложившуюся ситуацию по полочкам, можно использовать так называемую «вопросную матрицу». Это модификация одного из методов когнитивно-поведенческой психотерапии.
Представьте себе матрицу (таблицу) размерностью 3 Х 3. Столбцы матрицы – это время: прошлое, настоящее и будущее. Строки матрицы – это измерения нашего опыта: чувства, мысли, действия. Всего получается девять вопросов, вдумчивые ответы на которые помогут нам разобраться в себе и наметить пути решения проблемы:
- Что я чувствовал (какие эмоции переживал) тогда, когда это случилось со мной?
- Какие мысли у меня возникли тогда в связи с данной ситуацией?
- Что я пытался сделать в данной ситуации?
- Что я чувствую по поводу всего случившегося сейчас, в настоящий момент?
- Какие мысли, идеи, соображения в связи с этим приходят в голову?
- Что я делаю в настоящее время, чтобы разобраться с ситуацией и решить проблему?
- Что бы мне хотелось чувствовать (какие эмоции переживать) по отношению к данной ситуации в будущем?
- Какие выводы/уроки/принципы из данной ситуации я мог бы вынести из этой ситуации в будущем?
- Как изменится мое поведение после всего произошедшего в будущем? Что я могу сделать для этого уже сейчас?
Ответы на эти девять вопросов можно дать в диалоге с психотерапевтом, но можно и самостоятельно.
Если отвечаете на них самостоятельно, то лучше не торопиться и давать эти ответы письменно. Идеальный вариант, если на каждый из вопросов вы даете не менее 4-5 ответов.
Делать это лучше всего не за один раз, а растянуть заполнение вопросной матрицы дня на 3-4. Такой неспешный подход помогает лучше осознать свое состояние, глубже погрузиться в решение проблемы.
Приглашаем на мастер-класс, который научит задавать себе правильные вопросы и «хакнуть реальность»:
Отвечать на вопросы лучше постепенно, двигаясь от прошлого к будущему. Как правило, когда начинаются ответы на вопросы о будущем, у отвечающего уже появляются конструктивные идеи о том, как пережить трудную жизненную ситуацию и что делать дальше. Но в любом случае лучше не торопиться, и работать с вопросной матрицей столько, сколько необходимо. Правильные вопросы и вдумчивые ответы на них обязательно приведут к решению проблемы!
Полезно? Поделись статьей в Вконтакте или Фейсбук в 1 клик!
20 лет «Матрице»: Почему сюжет фильма до сих пор актуален?
31 марта исполнилось 20 лет с момента выхода фильма «Матрица».
Научно-фантастический фильм был хитом кассовых сборов благодаря своей футуристической атмосфере, необычным костюмам и инновационному сюжету. Фильм также послужил катализатором для массовой дискуссии вокруг некоторых философских тем, передает Quartzy.
Фильм рассказывает о хакере Нео, который узнает, что вся его жизнь была проведена в смоделированной реальности, разработанная искусственным интеллектом.Сценарий напоминает один из самых длительных экспериментов западной философии. В известном отрывке из Republic Платона (около 380 г до н. э.) предполагается, что человеческая осознанность подобна группе заключенных, которые прожили свою жизнь под землей, а их жизненный опыт ограничен тенями, спроецированными на стенах тюрьмы.
Платон считал, что заключенный во время освобождения будет поражен, узнав правду о реальности, и ослеплен сиянием солнца.
Если он вернется обратно в пещеру, то спутники не смогут понять того, что он испытал и, несомненно, будут считать его сумасшедшим.
В «Матрице» Нео освобождается благодаря лидеру повстанцев Морфеусу (по иронии судьбы, имя обозначает греческого бога сна), впервые пробудившись в реальной жизни. Но в отличие от тюремных заключенных в теории Платона, которые обнаруживает «высшую» реальность за пределами своей пещеры, Нео в своей реальности видит, насколько ужасен и опустошен его внешний мир.
Ошибочная осознанность
«Матрица» также фокусируется на более сложных философских вопросах, которые были заданы французом XVII века Рене Декартом. Он рассуждал по поводу человеческой осознанности, уверенности в наших чувствах и способности понимать и знать что-либо в этом мире.
Декарт даже отметил, что человеческая осознанность не является результатом какого-то сна или толчка. Соответственно, она разрабатывается в результате определенного пути в жизни.
Поэтому быть хоть в чем-то уверенным в мире очень сложно без каких-либо доказательств или знаний.
Что такое реальность?
Французский философ-постмодернист конца XX века Жан Бодрийяр, чья книга кратко появляется в начале самого фильма, много писал о том, как современное общество создает сложные имитации реальности. Они становятся настолько правдивыми, что их принимают за саму реальность. Пример: телевизор, картина или видео.
Конечно, для этого не нужен заговор искусственного интеллекта, как в «Матрице». Сейчас мы наблюдаем это, возможно, более интенсивно, чем 20 лет назад, оказавшись среди «реалити-шоу» и соцсетей.
В некоторых аспектах фильм достигает точки зрения, которая близка видению немецкого философа XVIII века Иммануила Канта. Он настаивал на том, что это не наши чувства копируют внешний мир, а сама реальность соответствует условиям нашего восприятия. Иными словами, мы ощущаем и видим мир через спектр наших чувств.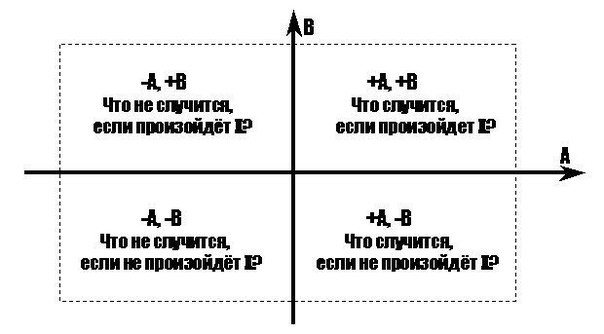
Этика свободы
В итоге трилогия «Матрица» провозглашает, что свободные люди могут изменить будущее. Но каким образом ощущается эта свобода?
Дилемма раскрывается в ситуации с красно-синей таблеткой первого фильма, поднимающая вопрос этики веры. Выбор Нео состоит в том, чтобы принять либо «действительно реальное» (на примере красной таблетки, которую ему предлагает Морфеус), либо вернуться к своей более нормальной «реальности» (через синюю таблетку).
Это затруднение было запечатлено в эксперименте 1974 года американским философом Робертом Нозиком. Он создал «машину опыта» способную передать любой опыт человеческому разуму. Таким образом, он ничем не отличается от «реального» опыта, но сам человек не получит его самостоятельно, а с помощью внушения машины. Встает вопрос: нужно ли выбирать правильную реальность или наслаждаться той, которую мы отберем?
В «Матрице» мы видим, что повстанцы решительно отвергают удобства матрицы, предпочитая мрачную реальность.
Но также есть мятежный предатель Сайфер, который отчаянно ищет реинтеграцию в приятную симулированную реальность.
Главный злодей фильма агент Смит (Хьюго Уивинг) мрачно отмечает, что человечество ненасытно потребляет природные ресурсы. Матрица, по его словам, является «лекарством» от этой человеческой «инфекции».
Мы много слышали о потенциальных опасностях искусственного интеллекта, но, возможно, в обвинении агента Смита что-то есть.
декартовых координат и матриц преобразования — Polymath Programmer
Если вы работаете в 3D, вам необходимо знать декартову систему координат и матрицы преобразования. Декартовы координаты обычно используются для представления мира в 3D-программировании. Матрицы преобразования — это матрицы, представляющие операции над трехмерными точками и объектами. Типичные операции — это перемещение, вращение, масштабирование.
Двумерные декартовы координаты
Вы должны были видеть что-то подобное в своем классе математики:
[исходное изображение]
Римские буквы I, II, III и IV представляют квадранты декартовой плоскости .
Например, III представляет третий квадрант. Здесь особо нечего сказать, так что продолжаем…
3-х мерные декартовы координаты
А для трех измерений у нас есть это:
[исходное изображение]
Мне не нравится, как ось Z направлена вверх. Идея, вероятно, связана с листом бумаги, представляющим двумерную плоскость, образованную осями x и y. Бумага кладется на плоский горизонтальный стол, ось z направляется вверх.
С математической точки зрения разницы нет.
Однако мне проще посмотреть на это так:
Декартова плоскость XY находится в вертикальном положении, представляя экран. Ось Z просто выступает из экрана. Окно просмотра может охватывать все четыре квадранта плоскости XY. На рисунке показан только первый квадрант, поэтому я не высовываю вам глаза осью Z * улыбка *
Существует также так называемое правило правой руки и, соответственно, правило левой руки . Правое правило имеет ось z, указывающую за пределы экрана, как показано выше.
Правило левой руки имеет ось z, указывающую на экрана. Соблюдайте правило правой руки:
Большой палец представляет ось x, указательный палец представляет ось y, а средний палец представляет ось z. Что касается правила левой руки, мы имеем:
Мы смотрим на другую сторону плоскости XY, но это то же самое. Ось z указывает в другом направлении. И да, у меня длинные пальцы. Моя рука может покрыть целую октаву на фортепиано.
В чем дело? Потому что ваш движок трехмерной графики по умолчанию может использовать определенное правило, и вы должны им следовать. В противном случае вы можете найти ошибки, например, почему объект не отображается на экране. Потому что объект находился за камерой, когда вы думали, что он впереди. Выбранный вами графический движок также должен позволять вам использовать другое правило, если вы того пожелаете.
Если вам интересно, вот иллюстрация правила справа с осью Z, направленной вверх:
Мне все еще не нравится, когда ось Z направлена вверх.
Меня это почему-то раздражает…
Масштабирование (или создание чего-то большего или меньшего)
Так как же увеличить или уменьшить что-либо в 3D? Вы применяете матрицу масштабирования. Давайте посмотрим на 2D-версию:
Если коэффициент масштабирования больше 1, вы увеличиваете объект. Если ваш коэффициент масштабирования меньше 1, вы уменьшаете объект. Как вы думаете, что произойдет, если ваш коэффициент масштабирования равен 1? Или когда у вас коэффициент масштабирования отрицательный?
Так как же коэффициент масштабирования выглядит в матрице масштабирования?
Если вы не знаете, что это означает, или не знаете, каким должен быть результат, просмотрите урок о матрицах и соответствующем программном коде.
Вы заметите, что существуют отдельные коэффициенты масштабирования для осей x и y. Это означает, что вы можете масштабировать их независимо. Например, у нас есть это:
А увеличиваем только по оси абсцисс:
Мы также можем увеличивать только по оси y:
Ага, мне надоело рисовать 2D картинки, поэтому я решил сделать несколько 3D.
Говоря об этом, теперь у вас должна быть возможность предложить 3D-версию матрицы масштабирования. Подсказка: просто добавьте масштабный коэффициент для оси z.
Вращение (или вращение до рвоты)
Вот как выглядит матрица вращения для двух измерений:
Тот символ, который выглядит как буква O с прорезью посередине? Это тета (произносится как th-ay-tuh), греческий алфавит. Обычно используется для обозначения неизвестных углов.
Я избавлю вас от математического вывода формулы. Просто используйте это.
Вы можете убедиться в этом, проведя простой эксперимент. Используйте вектор (1,0) или единичный вектор, лежащий на оси x.Подключите 90 градусов для теты, и вы должны получить (0,1), единичный вектор, лежащий на оси y.
Это вращение против часовой стрелки. Чтобы повернуть по часовой стрелке, просто используйте значение со сменой знака. Итак, у вас будет -90 градусов.
В зависимости от используемых математических библиотек, вам может потребоваться использовать радианы вместо градусов (что типично для большинства математических библиотек).
Я уверен, что вы достаточно сообразительны, чтобы самостоятельно вычислить формулу преобразования градуса в радиан…
Теперь самое сложное.3D-версия вращения… немного сложна. Видите ли, то, что вы прочитали выше, на самом деле вращается вокруг предполагаемой оси Z. Подождите, это означает, что вы можете вращаться вокруг оси x! И ось Y! Сакребле! Можно вращать вокруг любой произвольной оси !
Я напишу об этом еще одну статью. Если вам это нравится, возможно, вам стоит взглянуть на эту статью о 3D-вращении. Я также коснусь концепции, в которой вы вращаетесь вокруг одной оси, а затем вращаетесь вокруг другой оси. Будьте готовы к тому, что в формуле будет много синусов и косинусов.Перестань плакать; это неприлично с вашей стороны.
Перевод (здесь ничего лингвистического)
Это означает, что вы перемещаете точки и объекты из одного положения в другое. Давайте посмотрим на одномерный пример:
Волнистый, неустойчивый на вид подражатель? Это дельта греческого алфавита.
Дельта-x — это стандартное обозначение для «изменения x». В этом случае «x» означает расстояние по оси x. В оставшейся части нашего обсуждения мы будем использовать версию, которую проще набирать, под названием «dx».
В двух измерениях у нас есть соответствующая dy для «изменения y». Обратите внимание, что ничто не мешает вам использовать отрицательные значения для dx или dy. На рисунке выше dx и dy отрицательны.
Вы должны представить себе случай 3D, потому что диаграмма, вероятно, будет беспорядочной. Но это легко визуализировать. Сделайте то же самое для оси Z.
Так что же представляет собой матрица преобразования для перевода? Во-первых, вам нужно увеличить размер матрицы и размер вектора на одно измерение.Точные причины связаны с аффинными преобразованиями и однородными координатами (я кратко упоминал их ранее).
Учтите: у вас есть точка (x, y, z), и вы хотите, чтобы она находилась в новой позиции (x + dx, y + dy, z + dz). Тогда матрица будет выглядеть так:
Обратите внимание, что для масштабирования важными записями являются диагональные записи.
Для вращения есть синусы и косинусы, и они повсюду. Но для перевода «основная часть» матрицы на самом деле является единичной матрицей.Самое интересное происходит в столбце переулка в крайнем правом углу матрицы.
Это мне напомнило. Поскольку вы будете использовать все матрицы преобразования вместе, все матрицы должны быть одинакового размера. Таким образом, матрицы масштабирования и вращения тоже должны быть 4 на 4. Просто добавьте к ним ноль записей, кроме правой нижней записи, которая равна 1.
Заключение
Мы говорили о двухмерных и трехмерных декартовых координатах. Я также показал вам правила для правой и левой руки. Это формирует основу для изучения основных преобразований, таких как масштабирование, поворот и перенос.
Есть еще две интересные матрицы преобразования: сдвиг и отражение. Я думал, что то, что у нас есть, пока достаточно. Вы можете провести собственное исследование. Когда возникнет ситуация, я расскажу об этих двух трансформациях.
Если вам понравилась эта статья и вы нашли ее полезной, поделитесь ею со своими друзьями. Вам также следует подписаться, чтобы получать последние статьи (это бесплатно).
Эта статья о преобразовании между растровыми, декартовыми и полярными координатами может оказаться полезной.
Эти книги по «преобразованию координат» могут оказаться полезными.
Геометрия (Как работает матрица: Часть 2)
Геометрия
Связь между матрицами и декартовой системой координат
Если вы представите себе, что у вас есть точка \ (P_x \) с координатами (1, 0, 0), и вы хотите повернуть эту точку вокруг оси z на 10 градусов по часовой стрелке, то каковы будут координаты новой точки. Используя то, что мы узнали о матрицах вращения, мы знаем, что эти новые координаты можно найти с помощью простой тригонометрии.Координаты x новой повернутой точки задаются как cos (-10), а координата y — как sin (-10) (не забывайте, что тригонометрические функции в C ++ ожидают, что углы будут выражены в радианах).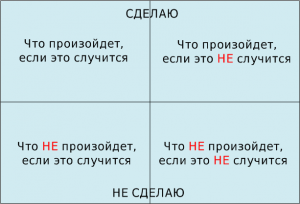
Если мы сделаем то же самое, но на этот раз с точкой \ (P_y \), которая равна (0, 1, 0), то координата x этой точки после поворота будет равна -sin (-10), а координата y будет быть равно cos (-10). Вы можете заметить, что первая строка (или строка) матрицы вращения, которая вращает точки вокруг оси z (\ (R_Z \)), содержит те же тригонометрические функции, что и те, которые мы использовали для вычисления новых координат точки \ (P_x \) после вращения.То же самое наблюдение можно сделать для второй строки матрицы, которая также содержит те же тригонометрические функции, что и те, которые мы использовали для вычисления новых координат для \ (P_y \):
Как вы можете видеть, когда мы вращаем эти оси вокруг z-вектора, новые координаты могут быть вычислены, используя для \ (P_x \) первую строку матрицы и для \ (P_y \), вторую строку.Если вы повторите упражнение для \ (P_z \) и матрицы вращения \ (R_X \) или \ (R_Y \), вы увидите, что новые координаты \ (P_z \) могут быть вычислены с использованием третьей строки любого из эти матрицы (в зависимости от того, вокруг какой оси вы вращаете \ (P_z \)).
Ключевая идея в понимании матриц состоит в том, что каждая строка матрицы представляет собой ось (или основания) системы координат. Это важно, так как позже вы узнаете, как создавать матрицы для преобразования точек и векторов из одной системы координат в другую (смена базиса), просто заменяя строки матрицы координатами каждой оси той системы координат, которую вы хотите изменить. преобразовать ваши векторы или точки в:
$$ \ begin {bmatrix} \ color {red} {c_ {00}} & \ color {red} {c_ {01}} & \ color {red} {c_ {02}} \\ \ color {green} {c_ {10}} & \ color {green} {c_ {11}} & \ color {green} {c_ {12}} \\ \ color {blue} {c_ {20}} & \ color {blue} {c_ {21}} & \ color {blue} {c_ {22}} \\ \ end {bmatrix} \ begin {array} {l} \ rightarrow \ quad \ color {красный} {ось x} \\ \ rightarrow \ quad \ color {зеленый} {ось Y} \\ \ rightarrow \ quad \ color {синий} {ось z} \\ \ end {массив} $$
Это распространенный метод компьютерной графики, который будет описан в следующих главах.
Матрицы становятся менее загадочными, когда вы понимаете, что они всего лишь способ хранения координат системы координат, где строки матрицы являются осью этой системы координат или матрицы ориентации , как мы иногда ее называем.
Ортогональные матрицы
Фактически, типы матриц, которые мы только что описали в этой и предыдущей главах (матрицы вращения), называются в линейной алгебре ортогональными матрицами .Ортогональная матрица — это квадратная матрица с действительными элементами, столбцы и строки которой составляют ортогональных единичных вектора . Ранее мы упоминали, что каждая строка матрицы представляет собой ось декартовой системы координат. Если матрица является матрицей вращения или результатом умножения нескольких матриц вращения друг на друга, то каждая строка обязательно представляет ось единичной длины (поскольку элементы строк построены из тригонометрических функций синуса и косинуса, которые используются для вычисления координаты точек, лежащих на единичной окружности).
T = I \)
, где I — единичная матрица (см. Главу «Матричные операции», чтобы узнать больше об инверсии матриц, транспонировании матрицы и матричной идентичности).
Аффинные преобразования
Иногда вместо матричного преобразования используются термины аффинные преобразования . Этот технический термин на самом деле более точен для обозначения преобразований, которые вы получаете при использовании типа матриц, который мы описали до сих пор. Короче говоря, аффинное преобразование — это преобразование, сохраняющее прямые линии. Сдвиг, поворот, матрица сдвига — все это аффинные преобразования, как и их комбинации.Другой тип преобразования, который мы будем изучать в компьютерной графике, называется проективными преобразованиями (перспективная проекция — это проективное преобразование). Как вы, возможно, догадались, такие преобразования не обязательно сохраняют параллелизм между линиями (см. Уроки по матрице перспективы и ортогональной проекции в разделе «Основы 3D-рендеринга»).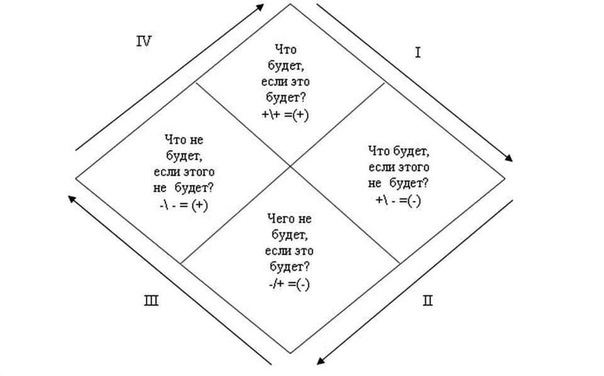
Резюме
Рис. 6: по мере вращения точки ее координаты относительно мировой системы координат (красная и зеленая оси) меняются.Но они остаются неизменными в отношении системы координат, определяемой матрицей вращения.
В этой главе (и в предыдущей) вы не только узнали, как создавать матрицы вращения, но мы также дали вам способ визуализировать, что такое матрица: каждая строка матрицы представляет одну ось декартовой системы координат. Ориентация (поворот), размер (масштаб) и положение (перемещение) этой системы координат представляют преобразование, которое будет применено к точкам, когда они умножаются на эту матрицу.Ключевая идея заключается в том, что точки изначально определены в определенной системе координат (назовем ее A). Если точка привязана к локальной системе координат B (матрице) и мы перемещаем, вращаем и перемещаем эту локальную систему координат (т.е. матрицу), координаты точки не изменятся относительно локальной системы координат B. каким-то образом ограничен преобразованием, применяемым к локальной системе координат B (он движется вместе с ней). Однако координаты этой точки изменятся в системе координат A.Умножение точки, координаты которой выражены относительно A, на матрицу B предоставит нам новые координаты точки в системе координат A. Это показано на рисунке 6.
Из этой главы вам нужно запомнить, как найти формулу для основных матриц вращения. Что важен порядок, в котором вы умножаете эти базовые матрицы. И наконец (и это почти самое главное), что матрицу можно рассматривать как локальную декартову систему, где каждая строка матрицы представляет одну ось этой локальной системы координат.Такая матрица также называется матрицей ориентации, и мы объясним почему в главе Создание матрицы ориентации или локальной системы координат.
Декартово МРТ-отпечаток в глазу на 7Т с использованием сжатого зондирования и реконструкций на основе завершения матрицы
Цель: Изучить осуществимость MR Fingerprinting (MRF) для быстрой количественной оценки времени релаксации в человеческом глазу при 7T, а также предоставить основу для сбора и обработки данных для будущей характеристики тканей у пациентов с опухолями глаза.
Методы: В этом подходе MRF с одноэлементной приемной катушкой с декартовой дискретизацией используется недостаточная дискретизация для сокращения времени сканирования и, следовательно, для уменьшения степени артефактов движения. Для реконструкции использовались подходы на основе сжатого зондирования (CS) и завершения матрицы (MC), в то время как их влияние на качество карт параметров MRF изучалось в ходе моделирования и экспериментов.Среднее время релаксации в глазу было измерено у 6 здоровых добровольцев. Один пациент с увеальной меланомой был включен, чтобы показать возможность MRF в клиническом контексте.
Полученные результаты: Результаты моделирования показали, что реконструкция на основе MC позволяет получить большие коэффициенты недостаточной выборки, а также дает более точные карты параметров по сравнению с использованием CS.
В экспериментах с 6 здоровыми добровольцами время сканирования было сокращено с 7:02 до 1:16 мин, что позволило получить изображения без видимой потери деталей в картах параметров при использовании реконструкции на основе MC.Время релаксации у 6 здоровых добровольцев согласуется со значениями, полученными при сканировании с полной выборкой, и значениями в литературе, а карты параметров у пациента с увеальной меланомой показывают четкую разницу во времени релаксации между опухолью и здоровой тканью.
Заключение: Декартово-основанное MRF возможно для глаза при 7Т. Высокие коэффициенты недостаточной дискретизации могут быть достигнуты с помощью MC, что значительно сокращает время сканирования и повышает комфорт пациента, а также снижает риск артефактов движения.
Ключевые слова: сжатое зондирование; высокое поле; магнитно-резонансная дактилоскопия; заполнение матрицы; визуализация глаз.
| Абстрактный базовый класс для записи преобразований. |
| Объединяет несколько преобразований вместе. |
| Выполняет преобразование тензорного устройства либо для всех атрибутов объекта |
| Преобразует атрибуты |
| Преобразует однородный или неоднородный граф в неориентированный граф, такой что \ ((j, i) \ in \ mathcal {E} \) для каждого ребра \ ((i, j) \ in \ mathcal {E} \). |
| Добавляет постоянное значение к каждому элементу узла |
| Сохраняет евклидово расстояние связанных узлов в атрибутах ребер. |
| Сохраняет относительные декартовы координаты связанных узлов в атрибутах ребер. |
| Сохраняет относительные декартовы координаты связанных узлов в атрибутах ребер. |
| Сохраняет полярные координаты связанных узлов в атрибутах ребер. |
| Сохраняет сферические координаты связанных узлов в атрибутах ребер. |
| Вычисляет пара точек, инвариантных к вращению. |
| Добавляет степень узла как одно горячее кодирование к характеристикам узла. |
| Сохраняет глобально нормализованную степень целевых узлов |
| Добавляет профиль локальной степени (LDP) из документа «Простая, но эффективная базовая линия для классификации графов без атрибутов» |
| Центрирует позиции узла на |
| Поворачивает все точки в соответствии с собственными векторами облака точек. |
| Центрирует и нормализует положение узлов до интервала \ ((- 1, 1) \). |
| Преобразует позиции узлов с помощью случайно выбранных значений перевода в заданном интервале. |
| Переворачивает позиции узлов вдоль заданной оси случайным образом с заданной вероятностью. |
| Преобразует позиции узлов |
| Масштабирует положение узлов с помощью случайной выборки коэффициента \ (s \) в заданном интервале, e.грамм. , в результате получается матрица преобразования |
| Поворачивает позиции узлов вокруг определенной оси с произвольно выбранным коэффициентом в пределах заданного интервала. |
| Сдвигает положения узлов с помощью произвольно выбранных факторов \ (s \) в пределах заданного интервала, например. , в результате получается матрица преобразования |
| Нормализует по строкам атрибуты, указанные в |
| Добавляет петли в данный однородный или неоднородный граф. |
| Удаляет изолированные узлы из графа. |
| Создает граф k-NN на основе позиций узлов |
| Создает ребра на основе позиций узлов |
| Преобразует грани сетки |
| Равномерно выбирает |
| Выбирает фиксированное количество из |
| Преобразует разреженную матрицу смежности в плотную матрицу смежности с формой |
| Добавляет две границы перехода к индексам границ. |
| Преобразует график в соответствующий линейный график: |
| Вычисляет наивысшее собственное значение лапласиана графа, заданное параметром |
| Создает векторы нормалей для каждого узла сетки на основе соседних граней. |
| Вычисляет триангуляцию Delaunay набора точек. |
| Преобразует изображение в суперпиксельное представление, используя изображение |
| Обрабатывает граф с помощью свертки диффузии графов (GDC) из статьи «Распространение улучшает обучение графам». |
| Модуль нейронной сети Scalable Inception Graph (SIGN) из статьи «SIGN: Scalable Inception Graph Neural Networks», который предварительно вычисляет фиксированные представления |
| Объединяет точки в воксели размером |
| Применяет нормализацию GCN из статьи «Полууправляемая классификация с графовыми сверточными сетями». |
| Уменьшение размерности узловых элементов с помощью разложения по сингулярным значениям (SVD). |
| Удаляет классы из обучающего набора на уровне узла, как указано в данных |
| Выполняет случайное разбиение на уровне узла, добавляя атрибуты |
| Выполняет случайное разбиение на граничном уровне на наборы для обучения, проверки и тестирования объекта |
Модули Quantum 1 - Утилиты модуля Quantum 1
Модули Quantum 1 - Утилиты модуля Quantum 1 B Утилиты модуля Quantum 1
Приложения квантовой механики часто используют представление внутренних координат Z-матрицы, а не стандартные декартовы координаты для описания моделей. Для приложений Quantum 1, которым это необходимо, Cerius 2 автоматически генерирует Z-матричное описание модели, которую необходимо изучить.Большинство приложений Quantum 1 предоставляют возможность манипулирования Z-матрицей, которая позволяет вам изменять структуру существующей модели, редактируя ее Z-матрицу. Они также предоставляют инструменты для переключения между декартовым представлением и представлением Z-матрицы и для добавления фиктивных атомов. В этой главе описывается
- Редактирование Z-матриц
- Добавление фиктивных атомов в модель
Редактирование Z-матриц Формат Z-матрицы - это метод представления структур модели с использованием внутренних координат.Z-матричное представление структуры определяет расположение атомов и связи между ними в терминах расстояний, углов и двугранных (торсионных) углов.
Cerius
2 Формат Z-матрицы Каждый атом в модели описывается отдельной строкой в определении Z-матрицы. Количество записей в каждой строке варьируется в зависимости от того, сколько атомов находится в модели и какие другие атомы уже определены (см. Рисунок 1). Например, длина связи не может быть указана до тех пор, пока не будут определены два атома; валентный угол не может быть указан до тех пор, пока не будут определены три атома.В следующих разделах описывается структура линий, образующих Z-матрицу Cerius 2 . Линия 1
Поскольку Z-матрица является внутренним представлением, в котором каждый атом описывается относительно других в структуре, первая строка просто определяет произвольно выбранный атом, который служит концептуальным источником матрицы. В первой строке появляются только две записи: номер строки и имя атома. Например, в модели перекиси водорода, показанной выше, где атом кислорода, которому присвоен порядковый номер один, выбран в качестве первого ссылочного атома, первая строка:
1 O1Этикетки Atom
Метки атомов Z-матрицы состоят из символа атома и порядкового номера атома, присвоенного Cerius 2 (например, C1, h5 и т. Д.).Чтобы отобразить серийные номера атомов Cerius 2 для вашей модели, выберите НОМЕРА во всплывающем окне метки атомов на главной панели управления визуализатора. Строка 2
Вторая строка в матрице определяет положение второго атома относительно атома, определенного в первой строке. Теперь можно определить расстояние между этими атомами. В строке появятся четыре записи. Они определяют номер строки (2), метку второго атома, длину связи и метку атома, с которым он связан (первый атом), в указанном порядке.(Фактически, эти атомы не обязательно должны быть связаны друг с другом, если, например, определяемый атом является фиктивным атомом или ионом металла. Однако проще описать Z-матрицу, как если бы все атомы были связаны как единая молекула.) Например, в модели перекиси водорода, показанной на рисунке 1, где другой атом кислорода, O2, связан с O1 связью длиной 1,402 Å и выбран в качестве контрольного атома для второй строки, строка 2 выглядит так:
2 O2 1,402 O1Строка 3
Третья строка в матрице определяет положение третьего атома относительно двух ранее определенных атомов.Теперь можно определить угол, образованный между двумя описанными связями. В строке появятся шесть записей. Они определяют номер строки (3), метку третьего атома, расстояние между третьим атомом и атомом, с которым он связан, образованный угол связи, метку атома, с которым атом связан, и метка последнего атома, которая описывает определенный валентный угол. Например, в модели перекиси водорода, показанной на рисунке 1, где атом водорода h4 связан с O1 связью длиной 0.999 Å, образуя валентный угол 99,82 ° между собой, O1 и O2, и выбран в качестве опорного атома для третьей строки, строка 3:
3 ч4 0,999 99,82 O1 O2Строки 4 и далее
Начиная со строки 4, можно полностью определить положения всех последующих атомов (каждый из которых, конечно, связан с одним из ранее определенных атомов). Торсионный угол (который описывает угол между плоскостью, образованной первым, вторым и третьим атомами, и плоскостью, образованной вторым, третьим и четвертым атомами), может быть определен на четвертой и всех последующих линиях.Восемь записей появляются в полных строках. Они описывают (не по порядку):
Например, в модели перекиси водорода, показанной на рисунке 1, существует только еще один атом, атом водорода (h5), и, следовательно, можно определить только одно кручение и одну полную линию. h5 соединен с O2 связью длиной 0,999 Å, образуя угол связи 99,81 ° между собой, O2 и O1, и угол кручения -180 ° между собой, O2, O1 и h4. Четвертая и последняя строка:. 4 ч5 0.999 99,81 -180 O2 O1 h4
Сводка формата Z-матрицы
Панель управления Z-Matrix Editor
Управление геометрией через Z-матрицу Панель управления Z-Matrix Editor (доступная при выборе пункта меню Geometry / Z-Matrix на многих картах Quantum 1) содержит элементы управления, которые позволяют создавать, просматривать и редактировать Z-матрицы. Используя Z-Matrix Editor, вы можете автоматически или вручную построить Z-матрицу для текущей модели.После того, как Z-матрица полностью построена (или если она уже существует), вы можете просмотреть матрицу, исследовать связность Z-матрицы вашей модели и изменить геометрию модели, изменив длины связей, углы и скручивания, которые определяют матрица.
Редактор Z-матрицы также предоставляет доступ к служебной программе, которая позволяет переключаться между декартовым и Z-матричным представлением атомов в модели.
Панель управления Z-Matrix Editor при первом открытии может выглядеть примерно так:
:
Осторожность
В списке Z-матрица отображается Z-матрица для текущей модели.Если здесь не отображается ничего, кроме списка чисел (как показано выше), нажмите кнопку ЗАВЕРШИТЬ Z-матрицу линий , чтобы сгенерировать Z-матрицу для вашей модели. Список должен теперь выглядеть примерно так:
Вы можете выбрать одну или несколько строк из списка Z-матрицы для редактирования, используя обычный механизм выбора с помощью мыши (см. Cerius 2 Среда моделирования , если вы еще не знакомы с выбором элементов в списках) . Использование редактора
Вы можете редактировать значения связи, угла и скручивания выбранных линий в Z-матрице, вводя значения в поля под полем списка Z-матрицы.Используйте спецификаторы Z-матрицы (поля ввода, которые соответствуют заголовкам столбцов, показанным в сводной таблице формата Z-матрицы под Сводка формата Z-матрицы), чтобы указать новые значения для строк, выбранных из списка Z-матрицы.
Эти элементы управления включают несколько, которые работают аналогично:
- Для всех этих элементов управления вы можете выбирать и редактировать несколько строк, используя одно и то же представление; линии, использующие разные представления, нельзя редактировать вместе.
Декартовы представления и представления Z-матрицы
Редактор Z-Matrix Cerius 2 поддерживает спецификацию и редактирование структур модели в формате, который сочетает в себе декартовы координаты и спецификации Z-матрицы.Такие смешанные представления могут быть полезны для определения моделей, для которых одни части легче задавать в декартовых координатах, а другие легче описывать в формате Z-матрицы. Элементы управления на панели управления декартовой Z-матрицей позволяют вам свободно изменять записи в списке Z-матриц панели управления Z-Matrix Editor между двумя представлениями. Панель управления с декартовой Z-матрицейПанель управления декартовой Z-матрицей (доступ к ней осуществляется щелчком по декартовой Z-матрице ... Кнопка на панели управления редактора Z-матрицы) содержит элементы управления, которые позволяют добавлять выбранные атомы в список Z-матрицы в декартовой нотации и изменять выбранные строки в списке между Z-матрицей и декартовым представлением. Информацию об элементах управления на этой панели управления см. В экранной справке.
Добавление фиктивных атомов в модель Какие фиктивные атомы используются для
Фиктивные атомы, которые появляются в моделях Cerius 2 с меткой X, часто добавляются к моделям, чтобы упростить спецификацию ограничений или определений атомов Z-матрицы.Фиктивные атомы также часто необходимы для определения ограничений, которые неудобно или невозможно определить только с реальными атомами. Ограничения используются для обеспечения того, чтобы значения переменных оставались в определенных определенных пределах в ходе вычислений. Интерфейсы Quantum 1 предлагают три инструмента (доступных на панели управления фиктивных атомов), которые обеспечивают гибкость добавления фиктивных атомов с использованием декартовых координат или положений Z-матрицы или в соответствии с их относительным положением по отношению к атомам, выбранным в модели.
Панель управления Dummy Atoms
Чтобы получить доступ к панели управления фиктивных атомов, выберите пункт меню Geometry / Dummy Atoms на большинстве карт Quantum 1. Создание фиктивных атомовВы можете определить фиктивные атомы, указав их координаты самостоятельно:
- Чтобы создать фиктивный атом в определенном месте в декартовом пространстве, установите координаты x, y, z в верхнем поле ввода и нажмите кнопку действия Добавить атом в (x, y, x) .
- Чтобы создать фиктивный атом в точке относительно положений других атомов (т. Е. Определяемой внутренними координатами), сначала выберите три атома (см. Cerius 2 Среда моделирования , чтобы узнать, как выбрать более одного атома) , введите желаемые координаты в среднее поле ввода и нажмите Добавить атом в ( , , ) кнопку действия , где = расстояние, = угол и = двугранный угол.
- Чтобы создать фиктивный атом, расположенный в геометрическом среднем координатах любых двух или более атомов, выберите эти атомы в своей модели, убедитесь, что MID-POINT выбран во всплывающем окне в нижней части панели управления фиктивными атомами, и нажмите соответствующую кнопку Добавить атом на кнопке действия .
- Для создания фиктивного атома, расположенного на внутренней или внешней биссектрисе (т.е.(например, вдоль линии, разделяющей угол, определяемый тремя атомами), выберите три атома в своей модели, выберите ВНУТРЕННЯЯ БИСЕКТОР или ВНЕШНЯЯ БИСЕКТОР , соответственно, во всплывающем окне и нажмите соответствующую кнопку Добавить атом на кнопке действия . . Нет необходимости связывать три атома друг с другом.
- Чтобы создать фиктивный атом, расположенный вдоль перпендикуляра к линии, соединяющей два атома или к наиболее подходящей плоскости через три или более атомов, выберите два или более атомов в своей модели, выберите ПЕРПЕНДИКУЛЯР во всплывающем окне и щелкните соответствующий Добавить атом на кнопку действия .
Вы всегда можете исправить ошибки, выбрав фиктивный атом, а затем выбрав пункт меню Edit / Cut на главной панели управления визуализатором.
картезианского скептицизма в фильме «Матрица» - 646 слов
«Матрица », снятая братьями Вачовски в 1999 году, считается одной из классических фильмов ХХ века.Он сочетает в себе новаторские и креативные боевые сцены с впечатляющей компьютерной графикой и удивительно глубоким сюжетом, который заставляет усомниться в реальности существующего мира. Он содержит многочисленные ссылки на философов Древней Греции и Древнего Китая и черпает вдохновение из различных литературных произведений, таких как « 1984 » Джорджа Оруэлла, «Алиса в стране чудес» и «Призрак в доспехах» . Тем не менее, центральная часть сюжетной линии фильма построена на философской концепции, известной как картезийский скептицизм.Цель этой статьи - исследовать философское основание этой теории и увидеть, как она связана с основой, лежащей в основе The Matrix .
Что такое декартовский скептицизм?
Рене Декарт, выдающийся мыслитель эпохи разума, сформулировал концепцию, которая позже была названа его именем. Его идея возникла из 5-минутного испытания, которое представляет собой теорию, утверждающую, что миру вокруг каждого из нас всего 5 минут и что все, включая воспоминания и физические доказательства, было создано злым демоном с неограниченной силой создавать и разрушать.Теория была основана на том факте, что все пять чувств, которыми пользуется человек, можно обмануть, как это часто бывает в реальном мире. Чтобы распознать обман, человеку нужно проверить ощущение, чтобы отвергнуть и подтвердить его.
Основываясь на этой предпосылке, Декарт написал несколько книг, в которых он тщательно и кропотливо исследовал каждую мысль и убеждение, которые у него были, пока в конечном итоге не нашел одну основу, на которой он мог бы построить все с нуля. Эта основа подтверждала его собственное существование посредством сознательной мысли.«Я думаю, следовательно, я есть» - таков легендарный афоризм, которым стала известна Рене Декарт.
Связь между картезианским скептицизмом и матрицей
Предпосылка фильма взята прямо из первоначального предположения Рене Декарт, которое утверждает, что мир вокруг нас - ложь и что он был создан существом, обладающим почти всемогущей силой. чтобы сохранить статус-кво. Выбор для Нео в The Matrix - либо принять иллюзию как реальность вещей, либо вырваться наружу и посмотреть, как на самом деле устроен мир.Путь Нео такой же, как и у философа, поскольку они оба осмелились исследовать реальность своего окружения. В случае с Нео гипотеза оказалась верной, в то время как для Декарта она оказалась неверной. Он подтвердил реальность своего мира, деконструируя его, а затем восстанавливая, по одной вере за раз.
Концепция сновидения и реальности в матрице
Часть, где Нео просыпается от сна в своей комнате, также связана с аргументом Декарта против реальности вещей.Он сравнивает мир со сном, который чрезвычайно реалистичен и невозможно проснуться, если демон не позволит вам это сделать. Он утверждает, что некоторые сны способны эффективно обмануть все пять чувств, что позволяет нашей реальности быть их продолжением. Та же идея используется в The Matrix . Идеи мира сновидений принадлежат не только Декарту, поскольку аналогичные вопросы можно найти в трудах Платона, а также в риторических вопросах китайского философа Чжуанчжи.
Выводы
«Матрица » - один из самых креативных фильмов, появившихся в Голливуде в конце 1990-х - начале 2000-х. Их успех был обусловлен не только исключительной игрой актеров в сочетании с инновационными спецэффектами и компьютерной графикой, но и глубоким философским обоснованием. Благодаря непрерывному прогрессу в кибернетике, достигнутому в последние десятилетия, антиутопическая реальность, нарисованная братьями Вачовски, скорее всего, станет реальностью. Возможно, это уже есть, но мы об этом не знаем.
Это эссе о картезианском скептицизме в фильме «Матрица» было написано и отправлено вашим однокурсником. Вы можете использовать его в исследовательских и справочных целях, чтобы написать свою статью; однако вы должны процитировать это соответственно.Запрос на удаление
Если вы являетесь владельцем авторских прав на эту статью и больше не хотите, чтобы ваша работа публиковалась на IvyPanda.
Запросить удаление Нужен нестандартный образец Essay , написанный с нуля
профессионально специально для вас?
вращающихся декартовых систем отсчета
вращающихся декартовых систем отсчетаВращение декартовых систем отсчета
Координаты (восток, север) в кадре электронного тахеометра (ETS) опорная точка целевой точки может отличаться от относительных координат в UTM (Универсальная поперечная проекция Меркатора).Настоящий север трудно определить с точностью лучше пары градусов, и истинный север не обязательно то же самое, что север в нашей части сетки UTM.
Пусть на рисунке выше X и Y представляют систему отсчета ETS (X = восток, Y = север), а X и Y представляют систему координат карты (UTM) (карта востока и севера соответственно). ETS измеряет координату (x, y) в (X, Y) точка зрения. Как преобразовать эти (x, y) в правильные (x, y) координаты в системе координат карты (X, Y)?
Пусть θ = угол (измеренный против часовой стрелки) вращения, необходимого для того, чтобы ось X находилась в том же положении как ось X.Можно показать, что координаты (x, y) находятся путем вычисления
Коэффициенты, необходимые для поворота координат из (X, Y) в (X, Y), могут быть выражается как матрица вращения A
Пусть P (x, y) = матрица, состоящая из пар координат (восток и север). соответственно) из обзора EDM (x, y, z). Матрица P 'является произведением P * A (умножение матрицы P на матрицу A).