Общий знаменатель дробей | Математика
Это правило позволяет легко и быстро устно найти наименьший общий знаменатель дробей.
Правило нахождения наименьшего общего знаменателя для двух или нескольких дробей:
1) Выбираем из всех знаменателей наибольшее число и проверяем, делится ли оно на остальные. Если делится, то это число и есть наименьший общий знаменатель (НОЗ) этих дробей.
2) Если наибольший знаменатель не делится на все остальные, умножаем его на 2 и проверяем, делится ли полученное число на все остальные. Если делится, то это новое число и есть НОЗ.
3) Если после умножения на два новое число не делится на все остальные, наибольший из знаменателей умножаем на 3,4,5 и так далее до тех пор, пока новое число не будет делиться на все остальные. Это новое число и есть наименьший общий знаменатель.
Примеры.
Найти общий знаменатель дробей:
Выбираем бОльший знаменатель и проверяем, делится ли он на меньший.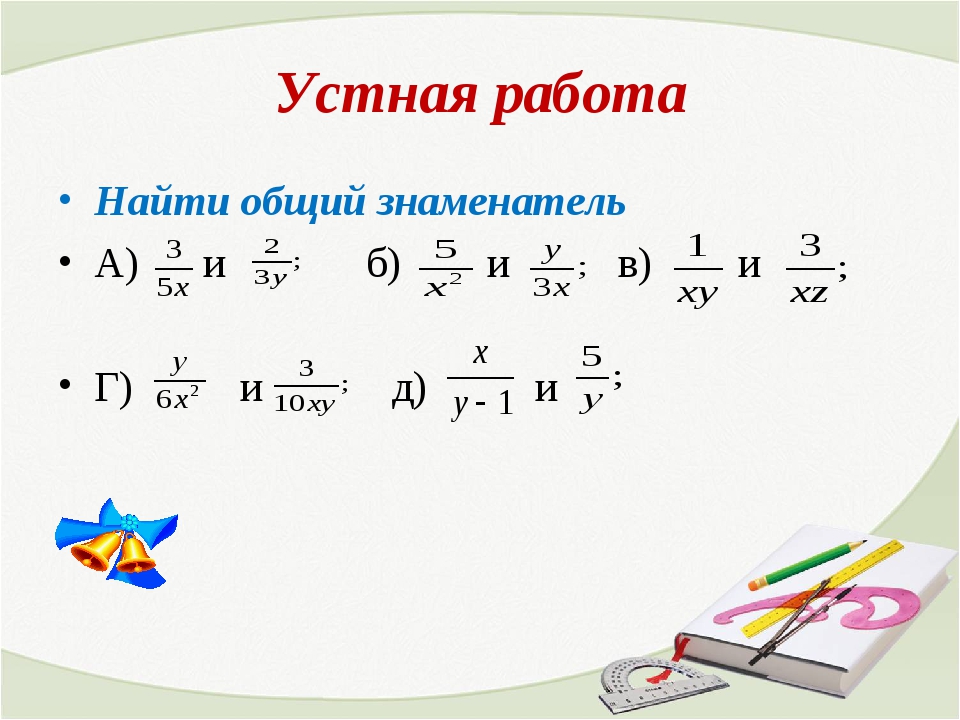
Выбираем больший знаменатель и проверяем, делится ли он на меньший. 15 на 10 не делится. Умножаем бОльший знаменатель на 2 и проверяем, делится ли новое число на меньший знаменатель. 15∙2=30, 30 на 10 делится. Значит, наименьший общий знаменатель этих дробей равен 30.
Выбираем большее число и проверяем, делится ли оно на остальные. 20 на 15 и 12 не делится. Большее число умножаем на 2 и проверяем, делится ли новое число на остальные. 20∙2=40. 40 на 15 и 12 не делится. Значит, большее число 20 надо умножить на 3 и проверить, будет ли делиться результат на остальные. 20∙3=60. 60 делится и на 15, и на 12. Поэтому 60 — наименьший общий знаменатель этих дробей.
Большее — 18. Оно не делится на меньшее — 15. Умножаем большее на 2: 18∙2=36. 36 на 15 не делится. Умножаем большее на 3: 18 ∙3=54. 54 на 15 не делится. Умножаем большее на 4: 18∙4=72. 72 на 15 не делится. Умножаем большее на 5: 18∙5=90. 90 на 15 делится. Значит, наименьший общий знаменатель этих дробей равен 90.
Умножаем большее на 5: 18∙5=90. 90 на 15 делится. Значит, наименьший общий знаменатель этих дробей равен 90.
В следующий раз мы посмотрим, как это правило применять при сложении и вычитании дробей с разными знаменателями.
Как найти наибольший общий делитель (НОД) + свойства, формулы
Понятие наибольшего общего делителя
Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.
Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4.
Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.
Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).
Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:
Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.
- Зафиксируем все делители четырех: ±4, ±2, ±1.

- А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
- Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.
Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.
Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.
Еще один пример. Рассчитаем НОД для 28 и 64.
Как находим:
- Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
- Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Свойства наибольшего общего делителя
У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.
Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.
Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.
Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.
Доказательство Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b. В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.
|
Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.
- Например, НОД (4, 40) = 4, так как 40 кратно 4.
Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.
Доказательство Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c. Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым. |
Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).
Доказательство Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители. |
Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.
Способы нахождения наибольшего общего делителя
Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.
1. Разложение на множители
Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.
Пример 1. Найти НОД (84, 90).
Как решаем:
- Разложим числа 84 и 90 на простые множители:
- Подчеркнем все общие множители и перемножим их между собой:
2 * 3 = 6.

Ответ: НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Как решаем:
- Разложим 15 и 28 на простые множители:
- Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
Ответ: НОД (15, 28) = 1.
Пример 3. Найти НОД для 24 и 18.
Как решаем:
- Разложим оба числа на простые множители:
- Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.
- Перемножим общие множители:
НОД (24, 18) =2 * 3 = 6
Ответ: НОД (24, 18) = 6
2. Алгоритм Евклида
Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.
Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.
Пример 1. Найти НОД для 24 и 8.
Как рассуждаем:
Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.
В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:
- Большее число поделить на меньшее.
- Меньшее число поделить на остаток, который получается после деления.
- Первый остаток поделить на второй остаток.
- Второй остаток поделить на третий и т. д.
- Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.
Пример 2. Найти наибольший общий делитель чисел 140 и 96:
Найти наибольший общий делитель чисел 140 и 96:
Как решаем:
- 140 : 96 = 1 (остаток 44)
- 96 : 44 = 2 (остаток 8)
- 44 : 8 = 5 (остаток 4)
- 8 : 4 = 2
Последний делитель равен 4 — это значит: НОД (140, 96) = 4.
Ответ: НОД (140, 96) = 4
Пошаговое деление можно записать столбиком:
Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:
- Найти наибольший общий делитель любых двух чисел из данных.
- Найти НОД найденного делителя и третьего числа.
- Найти НОД последнего найденного делителя и четвёртого числа и т. д.
Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.
Лучший друг. Как найти общий язык со своим ребенком
Родительская любовь и забота — еще не гарантия хороших отношений в семье и правильного воспитания. Сложнее всего найти общий язык и наладить обратную связь с ребенком. Таких «мостиков» может быть множество, а один из важнейших — формирование интеллекта и самостоятельного мышления. И хотя развитие детей строго индивидуально, эти пять общих принципов помогут создать сильную, позитивную и развитую личность.
Сложнее всего найти общий язык и наладить обратную связь с ребенком. Таких «мостиков» может быть множество, а один из важнейших — формирование интеллекта и самостоятельного мышления. И хотя развитие детей строго индивидуально, эти пять общих принципов помогут создать сильную, позитивную и развитую личность.
Если мы хотим, чтобы ребенок нас слышал, мы должны слушать его. Он будет делать то, что делаем мы, и если мы не обращаем внимания на слова ребенка и все решаем за него, он будет поступать так же.
Самый действенный способ наладить контакт — совместные игры и решение задач. Можно придумать интересный квест с поиском записок или предметов дома, можно играть с детьми в разгадывание «шифровок», которые они так любят. Кстати, обратную связь отлично подкрепляет игра в цвета — когда вы заранее договариваетесь раз в день вешать на стену или на календарь разноцветные бумажки, где каждый цвет обозначает определенное настроение. В общем, все зависит от вашей фантазии.
В общем, все зависит от вашей фантазии.
Реклама на Forbes
Вы наверняка замечали, что дети охотно объясняют взрослым то, в чем разбираются лучше их. Вместе осваивать новые сложные игры и решать задачи — отличный вариант совместного досуга с ребенком. Например, многие родители помнят, как двигаются шахматные фигуры, но никогда не погружались в тонкости шахматного искусства и не знают, чем отличается дебют от эндшпиля. Начав вместе по книгам постигать шахматные премудрости, вы можете вскоре обнаружить, что ребенок разбирается в игре гораздо лучше вас. Ничто так не поднимает детскую самооценку, как умение решать определенные задачи лучше взрослых.
2. Ставьте выполнимые задачиРазвивая ребенка в определенном направлении — искусстве, спорте или науке, многие родители начинают торопить события и завышать ожидания. Одна из самых частых родительских ошибок — обещания, что если ребенок выиграет соревнования, выполнит сложное задание или получит отличную оценку по предмету в школе, то непременно станет великим художником, спортсменом или ученым. Этого, скорее всего, не случится, но такое обещание фиксируется детским подсознанием, а затем наступает разочарование.
Этого, скорее всего, не случится, но такое обещание фиксируется детским подсознанием, а затем наступает разочарование.
Важно сформировать у ребенка верную самооценку, а это положительное соотношение достигнутого успеха к ожидаемому результату. Поэтому и ожидания должны быть реальными и даже чуть заниженными — ведь маленькому человеку очень важно ощутить уверенность в своих силах. На многих детских спортивных соревнованиях тренеры вводят дополнительные номинации: «За достойное поведение», «За волю к победе», «За красивую игру». Так каждый ребенок получает реальное поощрение своих наилучших качеств.
Помните, что в любом деле главное — спокойное поступательное движение, без сверхзадач и обязательных рекордов. Также надо постараться не обесценивать реальные достижения ребенка и не дать развиться «внутреннему критику», который обязательно появится, если постоянно негативно оценивать успехи ребенка, и тем более — сравнивать его достижения с успехами других детей.
3. Развивайте интеллект и внимательность
Развивайте интеллект и внимательностьВсе дети непоседы от природы. Дошкольники активно познают окружающий мир, легко переключаются с одного занятия на другое и ни минуты не сидят на месте. Это нормально, но если не приучить ребенка с раннего детства концентрировать внимание на выполнении одной задачи, потом могут возникнуть трудности с освоением важных навыков и обучением.
Основной метод развития внимания и усидчивости — игровой. Это может быть рисование, лепка, сбор пазлов или помощь по хозяйству: важно, чтобы процесс не утомлял и был интересен. Если через 10-20 минут занятия ребенку стало скучно — не нужно заставлять его продолжать, можно переключиться на другую игру, а к этой вернуться позже. Но постарайтесь в результате доводить каждое дело до конца.
Разумеется, дисциплина, порядок, привычка к определенным ритуалам и режиму дня защищают детскую психику и воспитывают характер. А характер и есть будущая судьба ребенка.
4. Соблюдайте меру в похвалах и наказанияхКонечно, хвалить ребенка нужно всегда, но не по мелочам, чтобы не пропала ценность поощрения. Важно, чтобы малыш понимал, за какие конкретные действия его хвалят. Не ленитесь объяснять каждый раз, что именно ребенок сделал правильно, и подкреплять похвалу тактильно — приласкать, обнять, поцеловать. Важно донести до ребенка, что объект любви — он сам, а не его успехи и достижения. Только тогда ребенок чувствует себя в безопасности и может развиваться позитивно, без тревожности и эмоционального дискомфорта.
Важно, чтобы малыш понимал, за какие конкретные действия его хвалят. Не ленитесь объяснять каждый раз, что именно ребенок сделал правильно, и подкреплять похвалу тактильно — приласкать, обнять, поцеловать. Важно донести до ребенка, что объект любви — он сам, а не его успехи и достижения. Только тогда ребенок чувствует себя в безопасности и может развиваться позитивно, без тревожности и эмоционального дискомфорта.
Часто тревожность — это результат неправильной системы поощрений и наказаний. Понятно, что рукоприкладство и игнорирование ребенка в ответ на неправильный поступок в сегодняшнем мире неприемлемы. Гораздо эффективнее работает «разбор полетов», когда вы вместе с ребенком спокойно и поэтапно выясняете, что именно случилось, и вместе ищите пути исправления ошибки. Только так ребенок может сам нащупать верную модель поведения, а вы не потеряете авторитет в его глазах и останетесь для малыша мудрым советчиком и верным другом — ведь друзья друг друга не наказывают.
5. Прислушайтесь к советам педагогов
Прислушайтесь к советам педагоговВ отличие от родителей, которые безоговорочно любят своего ребенка, педагоги и тренеры воспринимают его со стороны, а значит, более объективно. Хороший воспитатель увлечен своей работой и мотивирован на рост своих учеников в той области, которую представляет. Он всегда разработает лучший план обучения для каждого воспитанника, которому родители и ребенок должны неукоснительно следовать, чтобы получить желаемый результат.
Одна из важнейших задач, которую решают тренеры и воспитатели, и которая редко решается в семье — научить ребенка мириться с неудачами и идти дальше. Уметь проигрывать так же важно как уметь побеждать, и профессионалы учат этому лучше, чем близкие родственники.
Воспитывая характер и развивая интеллект ребенка, наверное, важнее всего помнить, что дети есть дети, и развитие мышления это не только обучение математике и иностранным языкам, а физическое развитие — не только спортивные победы и выигранные кубки и грамоты. Полноценное развитие дает ребенку только познание мира во всех его красках и проявлениях, полноценное общение со сверстниками, шумные игры, а также ссадины, синяки и ошибки, на которых все мы учимся независимо от возраста.
Полноценное развитие дает ребенку только познание мира во всех его красках и проявлениях, полноценное общение со сверстниками, шумные игры, а также ссадины, синяки и ошибки, на которых все мы учимся независимо от возраста.
Как найти общий язык со сверстниками? — Психология
Как найти общий язык со сверстниками? Как стать интересным собеседником? Сегодня будут несколько рекомендаций как же это сделать. Для того, что бы быть интересным собеседником, нужно научиться слушать. Порой желая произвести впечатление на других, можно много говорим о себе и забывать слушать. Или стать просто слушателем, не поддерживая беседу. Как же найти «золоту середину» в общении. А это важно. Когда слушаешь, постарайся не замыкаться. Не скрещивай рук и старайся собеседнику дать понять, что ты его слышишь. Например, можно кивать головой. Если ты чего то не понимаешь, то в любой момент можешь задать вопрос. Это абсолютно нормально. Именно так ты поддерживаешь интересную беседу. Если твое мнение отличается, от того что говорит собеседник, то все равно нужно дослушать его до конца. А потом всегда можно сказать, да я тебя понимаю, но думаю по-другому, и высказать свою точку зрения. Не избегай контакта взглядами. Помни, очень важно что бы они находились на одном уровне. Так, если твой собеседник сидит, то ты тоже сядь, а если стоит, то лучше встать. Так общаться будет намного комфортнее.
А потом всегда можно сказать, да я тебя понимаю, но думаю по-другому, и высказать свою точку зрения. Не избегай контакта взглядами. Помни, очень важно что бы они находились на одном уровне. Так, если твой собеседник сидит, то ты тоже сядь, а если стоит, то лучше встать. Так общаться будет намного комфортнее.
Как правильно выбирать друзей. Присмотрись внимательно вокруг. Может быть, рядом есть человек, с которым ты хотел бы дружиться. Что именно тебя в нем привлекает. Не стоит дружить с человеком, просто по тому что он популярный, например. Но если его убеждения и ценности тебе близки, то тогда вы легко найдете общий язык. И вам в дружбе будет интересно и комфортно. Если у тебя нет друзей, то стоит проанализировать эту ситуацию. Возможно, порой ты что-то делаешь не так. Измени в таком случае поведение. Но не отказывайся от своих убеждений и взглядов, оставайся самой собой. Старайся больше общаться. Общаться имеет смысл даже тогда, когда ты не рассматриваешь человека как свою подругу или друга. Ведь когда мы разговариваем и выполняем какие-то общие дела, мы узнаем лучше друг друга. и дружба может появиться неожиданно.
Ведь когда мы разговариваем и выполняем какие-то общие дела, мы узнаем лучше друг друга. и дружба может появиться неожиданно.
Главное помните, что не стоит навязываться и пытаться подружиться с теми, кто на самом деле не так уж и нравится.
Статья написана Тимофеевой Антониной Юрьевной педагог-психологом ЦСППСиМ РС(Я)
Как найти общий язык с ребенком-подростком: пять универсальных советов для родителей
Когда подростка наказывают за плохую отметку в школе, он грубит. Не пускают гулять — он убегает: «Я взрослый, сам могу решать, что и как мне делать», «Не желаю жить под вашу диктовку» — такие обвинения часто летят в сторону родителей. Почему еще вчера милый и вежливый ребенок буквально на глазах превращается в невоспитанного грубияна, объясняет Александра Палашина, завотделением ранней профилактики семейного неблагополучия семейного центра «Гармония».
Такими действиями ваш ребенок пытается заявить окружающему миру о себе, о том, что он повзрослел. Подросток стремится изменить свой статус в семье и в обществе. А родители по-прежнему все еще видят в нем маленького ребенка, и потому некоторые из них стремятся ограничить детскую свободу, чтобы не выпускать отпрыска из гнезда.
Подросток стремится изменить свой статус в семье и в обществе. А родители по-прежнему все еще видят в нем маленького ребенка, и потому некоторые из них стремятся ограничить детскую свободу, чтобы не выпускать отпрыска из гнезда.
«Повышенная конфликтность подростка, обидчивость и нередко плохое настроение и раздражительность часто бывают следствием серьезных внутренних перестроек. Грубость и вспыльчивость — это результат расхождения между тем положением, которое ребенок стремится занимать, и тем, которое он занимает фактически», — объясняет Палашина.
Как действовать родителям
- Дайте ребенку почувствовать себя значимым.
Дайте подростку понять, что его мнение очень важно для вас. Часто своим бессмысленным протестом он хочет добиться того, чтобы с его мнением считались и принимали как равного.
- Учитесь доверять ему.
Допустим, он обещал что-то сделать к определенному сроку. Не надо постоянно напоминать ему об этом. Особенно если вы знаете, что у вашего ребенка хорошая память. Займитесь своими делами, а его предоставьте самому себе.
Не надо постоянно напоминать ему об этом. Особенно если вы знаете, что у вашего ребенка хорошая память. Займитесь своими делами, а его предоставьте самому себе.
- Ослабьте контроль.
Не стоит постоянно контролировать подростка, чтобы он не сделал вдруг чего-то плохого. Эффективность такого способа воспитания будет не слишком высокой. Ваш ребенок, скорее всего, будет все делать наоборот, что только усилит недопонимание между вами. Чем больше вы будете давить на него, тем больше вероятность, что он сделает именно то, что вы ему запрещаете.
- Чаще вспоминайте себя в этом возрасте.
Даже если вы были совсем другим, то подумайте: неужели вам никогда не хотелось делать не то, что говорят родители? Возможно, это поможет понять его и принимать его таким, какой он есть, со всеми достоинствами и недостатками.
- Не прекращайте искать в нем хорошее.
Найдите в своем дорогом подростке хорошие качества и говорите ему о них. Даже не сомневайтесь: скоро эта ваша убежденность перейдет и к нему. А когда подросток уважает себя, он уважает и своих родителей.
Даже не сомневайтесь: скоро эта ваша убежденность перейдет и к нему. А когда подросток уважает себя, он уважает и своих родителей.
Источник публикации
Пресс-служба Департамента труда и социальной защиты населения города Москвы
Как найти общий язык с «трудными» коллегами
«Поведению можно научиться, — говорит Стефан Дилчерт, доцент кафедры менеджмента в Колледже Баруха. — То, что вас у есть определенная индивидуальность, не означает, что вы не можете вести себя иначе».
Чтобы определить, какие черты характера наиболее сильно выражены у человека, используют личностные тесты. Узнав результаты и предположив, как можно классифицировать коллег, можно понять, как строить межличностные отношения на работе. Например, тест «Большой пятерки» предлагает классификацию по пяти качествам: экстраверсии, доброжелательности, открытости опыту, добросовестности и эмоциональности.
У большинства характеристики выражены в рамках спектра. Но если у двух людей одна и та же характеристика выражена полярно, у них могут возникнуть трудности при совместной работе. Столкнувшись с человеком, чья личность контрастирует с вашей, не пытайтесь изменить его. Вместо этого используйте одну из следующих стратегией.
Но если у двух людей одна и та же характеристика выражена полярно, у них могут возникнуть трудности при совместной работе. Столкнувшись с человеком, чья личность контрастирует с вашей, не пытайтесь изменить его. Вместо этого используйте одну из следующих стратегией.
Люди, которые кажутся эгоистичными
Такие личности, как правило, набирают более низкие баллы по степени доброжелательности. Часто может показаться, что они думают только о себе. Они даже могут проявлять токсичное поведение, например, приписывать себе заслуги за работу другого товарища по команде или проявлять другие нарциссические черты личности.
«Некоторые нарциссы могут сильно вредить работе, — отметил сотрудник Fast Company и профессор психологии Арт Маркман. — Поэтому важно уметь различать людей, которые действуют уверенно, и тех, кто является настоящими нарциссами».
Для этого он советует обращать внимание на неспособность признавать чужие идеи (или склонность присваивать их) или попытки демонстрировать ложный авторитет.
Руководителю стоит напрямую обратиться к таким сотрудникам. Если они продолжают безжалостно переступать через других для достижения своих собственных целей, дайте им понять, что пора пересмотреть поведение, или готовьтесь уволить их ради сплоченности команды. Чтобы покончить с токсичным поведением, крайне важно продемонстрировать нулевую терпимость.
Люди, которые стремятся к конфликтам
Межличностным конфликтам не место на работе. Даже в небольших дозах они могут создавать напряженность и сказываться на результатах.
Тем не менее, некоторые споры могут быть полезны или, по крайней мере, не вредны для культуры компании.
«Конфликт — это реальность, с которой мы сталкиваемся на рабочем месте каждый день. По сути, в этом нет ничего плохого, — говорит Дилчерт. — Но межличностный конфликт — это то, чего мы должны избегать и не должны создавать».
Если возможно, дайте таким сотрудникам возможность работать над отдельными проектами. Постарайтесь донести до них, что успех каждого зависит от успеха команды. Не мешайте задавать друг другу вопросы и не концентрируйтесь на личностях. Таким образом, ни один конкретный человек не сможет проявлять неосмотрительное поведение, которое навредит группе.
Постарайтесь донести до них, что успех каждого зависит от успеха команды. Не мешайте задавать друг другу вопросы и не концентрируйтесь на личностях. Таким образом, ни один конкретный человек не сможет проявлять неосмотрительное поведение, которое навредит группе.
Люди, которые не прилагают усилий, чтобы нравиться
С доброжелательными сотрудниками легко ладить, они открыты для остальных членов команды не только как профессиональный ресурс, но и как друзья.
Если кто-то из коллектива не любит групповую работу и часто отвергает идеи, стоит обратить на него внимание. Менее доброжелательные люди не чувствуют себя так неловко, подводя людей, как доброжелательные. Поэтому постарайтесь предоставлять обратную связь как можно прямолинейнее. Не пытайтесь чрезмерно угодить им. Они могут не оценить то, что вы делаете, или не понять, почему вы это делаете.
Часто эти люди очень ориентированы на результат. Лицензированный терапевт Мелоди Уайлдинг советует использовать это и быть конкретнее. Объясните, в чем состоят трудности, и какие могут быть последствия.
Объясните, в чем состоят трудности, и какие могут быть последствия.
Полезно также призвать на помощь других коллег, который поддерживают конструктивный обмен идеями. Выбирайте для обсуждений формат круглого стола, чтобы авторитарный сотрудник не мог управлять беседой.
Люди, которые плохо справляются со сроками
Одна из характеристик теста «Большой пятерки» — добросовестность. На одном конце шкалы находятся те, кто взвешивает свои решения и способен доводить свои действия до конца, а на другом — несознательные личности, для которых не так важно соблюдать дедлайны и выполнять обязательства.
Они не чувствуют внутреннего побуждения следовать правилам. Они могут показаться ненадежными или неорганизоваными и предпочитают делать все по-своему, а не следовать установленным стандартам. Конечно, это не всегда плохо, но это может раздражать в условиях сжатых сроков.
Для работы с этими людьми стоит менее строго относиться к соблюдению сроков и организационных стандартов. Они могут не понимать, как важно быстро ответить на запрос коллеги, но могут смотреть на вещи по-другому, если они знают, что начальник команды проверит индивидуальные результаты через определенное количество дней. Другими словами, внедрите стратегии контроля.
Они могут не понимать, как важно быстро ответить на запрос коллеги, но могут смотреть на вещи по-другому, если они знают, что начальник команды проверит индивидуальные результаты через определенное количество дней. Другими словами, внедрите стратегии контроля.
Вне зависимости от наших индивидуальных особенностей в наших силах управлять своим поведением. Выберите правильную стратегию ради высоких результатов.
Источник.
Фото на обложке: fizkes / Shutterstock
Непростой ученик. Психолог о том, как найти общий язык с трудным подростком | образование | ОБЩЕСТВО
За время учебного года семьи разучаются проводить время вместе, а школьные трудности их порой заставляют становиться врагами. Поэтому лето — хорошее время снова научиться жить дружно и найти общий язык со своим ребенком.
Кто такие трудные подростки, и стоит ли их отчислять из школ? Почему 30 учеников в классе — это перебор? И отчего в России так плохо приживается инклюзивное образование, — рассказала к. п. н., доцент кафедры психологии развития и образования РГПУ им. А. И. Герцена, психолог отдела профилактики безнадзорности и правонарушений несовершеннолетних СПб ГБУСО социальный приют для детей «Транзит» Юлия Пежемская.
п. н., доцент кафедры психологии развития и образования РГПУ им. А. И. Герцена, психолог отдела профилактики безнадзорности и правонарушений несовершеннолетних СПб ГБУСО социальный приют для детей «Транзит» Юлия Пежемская.
Услышать каждого
Ольга Сальникова, SPB.AIF.RU: Говорят, что проблемными детьми не рождаются, а становятся. В чем же причины девиантного поведения некоторых подростков?
Юлия Пежемская: Здесь важно понять, кто же такой трудный ребенок. Это тот, кто неудобен и создает трудности для взрослых? Например, отстаивая свои права, пытаясь ослабить контроль и изменить мир в силу возрастного кризиса, который переживают большинство в период взросления. Многие творческие люди проходили через такой период, их отчисляли из школы, пророчили удручающее будущее, а сегодня они кумиры миллионов.
Или трудный — это тот, у кого есть проблемы с соматическим здоровьем? Ребенок часто болеет, вынужденно пропускает школу, не успевает, что приводит к определенным сложностям.
А может быть, у школьника психопатология, он не способен адаптироваться в классе из 30 человек и автоматически переходит в разряд непростых учеников?
И, наконец, если у ребенка проблемы в семье, ему тяжело живется, из-за стресса и конфликтов сосредоточиться на учебе невозможно — он тоже трудный?
Здесь можно провести аналогию со светолюбивым растением. Если посадить его в тень — оно не будет расти, но это не сорт плохой, а мы подобрали для него недостаточно подходящие условия. Поэтому если быть наблюдательными, любить детей, относиться к ним с уважением, создавать им необходимую атмосферу дома и в школе — число «трудных» учеников значительно уменьшится. И, безусловно, все эти дети имеют право на образование.
Фото: АиФ/ Вероника Такмовцева— А что делать, когда поступки некоторых учеников нарушают права на образование остальных детей?
— Мы привыкли реагировать, когда права уже нарушены, а до этого не задумываемся о проблеме. Потеря саморегуляции — один из признаков травматического опыта, показатель того, что человек нуждается в помощи. И санкциями (отчислением, переводом в другую школу) здесь ситуацию не исправишь. Я придерживаюсь позиции, что ребенок, у которого нет органических повреждений головного мозга, провоцирующих агрессивное поведение, — существо социальное и склонное к сотрудничеству. Тем более что такое поведение более выгодно для развития и благополучия, чем девиантное. Последнее же, как правило, связано с дефицитом удовлетворения какой-либо базовой потребности.
И санкциями (отчислением, переводом в другую школу) здесь ситуацию не исправишь. Я придерживаюсь позиции, что ребенок, у которого нет органических повреждений головного мозга, провоцирующих агрессивное поведение, — существо социальное и склонное к сотрудничеству. Тем более что такое поведение более выгодно для развития и благополучия, чем девиантное. Последнее же, как правило, связано с дефицитом удовлетворения какой-либо базовой потребности.
Поэтому работа с каждым учеником должна начинаться сразу при поступлении в школу, а не когда он уже нарушил права и потерял возможность управлять своим поведением.
В первую очередь это выражается в установлении контакта, пока его нет — ребенок в любой момент может стать трудным.
И здесь, с психологической точки зрения, идеальным вариантом была бы наполняемость классов до 15 человек (а не 30-35, как сейчас). Тогда учитель мог бы всех увидеть и услышать, с каждым договориться, учесть их потребности, а ребенок — проявить себя в школьной среде, почувствовать сопричастным и нужным. Наше внимание позволяет качественно работать лишь с небольшим количеством детей. Те, на кого ресурса не хватило, и могут оказаться в группе риска по девиантному поведению. Так как это еще и способ привлечь хоть какое-то внимание взрослого, пусть даже негативное.
Наше внимание позволяет качественно работать лишь с небольшим количеством детей. Те, на кого ресурса не хватило, и могут оказаться в группе риска по девиантному поведению. Так как это еще и способ привлечь хоть какое-то внимание взрослого, пусть даже негативное.
Дети хотят договариваться
— У вас был опыт исправления трудных учеников?
— Мы работали с петербургскими учениками, которых отчислили и не брали ни в какие другие школы. В течение августа они проходили реабилитационную программу, которая больше была направлена на межличностные отношения. Таким образом, у подростков выстраивалась новая модель отношений. Используя ее, они уже могли продолжать обучение в школе. Опыт оказался очень успешным. Дети учились более осознанно, формулировали свои цели, взаимодействовали с одноклассниками и учителями. Как правило, у каждого ребенка есть познавательная потребность получать знания, быть успешным, наладить хорошие отношения в школе. Нет детей, которые изначально приходят на уроки, чтобы плохо себя вести и получать двойки.
Более того, школьникам в принципе нравятся договорные и правовые отношения, но у взрослых зачастую нет времени их выстраивать. Мы живем иллюзией, что если у нас есть идеальные правила, то они подходят всем и нас обязаны слушать. Однако дети — мыслящие существа, они любят думать, задавать вопросы и бунтуют, когда им запрещают это делать. И если ребенок понимает, что его не будут ругать, критиковать, будут спрашивать всех по очереди (а не тех, кто всегда подготовлен к уроку), то есть его права соблюдаются, он не станет нарушать права других.
— Получается, что даже за один летний месяц можно изменить ситуацию?
— Если мы говорим о «трудных детях», контакт с которыми потерян, то важно попытаться за лето установить его. Если ваш ребенок будет знать, что нужен, ценен, любим, это позволит ему восстановить свои психологические ресурсы и вернуться в школу обновленным и вдохновленным, более устойчивым к трудностям. За время учебного года семьи разучаются проводить время вместе, школьные трудности их порой заставляют становиться врагами, поэтому лето — хорошее время снова научиться жить дружно.
Каждый, кто создает семью, — видит ее как свой ресурс, но ресурсы не бесконечны, их нужно учиться восполнять, совместно с детьми искать пути восстановления мира в семье и при необходимости обращаться за помощью. Как раз летом это сделать проще всего.
— Как правило, у трудных подростков трудные родители, но как их включить в процесс образования?
— Нужно устанавливать контакт. Если только обвинять, то родители откликаться не будут. Когда работа с классами организована правильно, взрослые легко вовлекаются. Это также показал наш опыт работы с трудными подростками в Санкт-Петербурге. Но сейчас учитель в силу своей перегруженности зачастую не готов к взаимодействию с родителями, даже с теми, кто стремится решить возникающие проблемы. Но здесь мы опять возвращаемся к проблеме переполненности классов.
Гибкая система
— А если девиантное поведение подростка связано с определенными диагнозами? Сейчас идет много споров про инклюзивное образование.
— Школа — это в какой-то мере модель общества, где есть разные люди, в том числе с особенностями развития. Мы не можем сделать вид, что их нет! Инклюзия — это способ позволить разным детям увидеть друг друга. Но существующая классно-урочная система плохо совместима с инклюзией, поэтому так много трудностей и споров по этому вопросу. В классно-урочной системе дети должны двигаться по программе в едином темпе: расти одинаково, достигать одинаковых образовательных результатов, которые измеряются также одними параметрами. Особенным ученикам трудно стать равноправной частью такой системы. В то время как, например, в системе Монтессори или в Вальфдорской школе это возможно, так как они в большей мере следуют за ребенком и его потребностями. Следуя за ФГОС (Федеральные государственные образовательные стандарты), важно не забывать про индивидуальный и дифференцированный подход к ученикам.
А то, чтобы в классе были дети с особенностями развития, на мой взгляд, очень важно и для обычных учеников «без диагнозов». Это позволит им развить эмпатию, лучше социализироваться в обществе, научиться договариваться и, как ни странно это звучит, быть успешнее в жизни и учебе. Ведь даже если собрать самый идеальный класс с высоким уровнем развития интеллекта у учеников и с прекрасными поведенческими навыками, спустя год учебы он расслоится. Кто-то обязательно будет успешнее, а отстающие начнут испытывать давление и чувствовать себя неудачниками. Поэтому не стоит прибегать к сегрегации с самого начала и дать возможность учиться всем вместе и выстраивать отношения.
Это позволит им развить эмпатию, лучше социализироваться в обществе, научиться договариваться и, как ни странно это звучит, быть успешнее в жизни и учебе. Ведь даже если собрать самый идеальный класс с высоким уровнем развития интеллекта у учеников и с прекрасными поведенческими навыками, спустя год учебы он расслоится. Кто-то обязательно будет успешнее, а отстающие начнут испытывать давление и чувствовать себя неудачниками. Поэтому не стоит прибегать к сегрегации с самого начала и дать возможность учиться всем вместе и выстраивать отношения.
Кстати
В 2020 году петербургские подростки совершили 443 преступления — на 7,5% меньше, чем годом ранее. В основном это кражи (особенно велосипедов и телефонов), правонарушения, связанные с употреблением спиртного и наркотических веществ, разбойные нападения, причинение вреда здоровью средней тяжести, угоны автотранспорта. Около 70% совершающих преступления в СПб — внешне благополучные дети, учащиеся школ, колледжей и техникумов, ранее не попадавшие в поле зрения правоохранительных органов.
Общий знаменатель
Ekbjz0LLKxI
Это самый простой из известных нам методов сложения и вычитания дробей!
Что такое знаменатель?
Знаменатель — это нижнее число в дроби.
Показывает, на сколько равных частей разделен предмет.
Что такое общий знаменатель?
Когда знаменатели двух или более дробей равны и совпадают с , они равны общим знаменателям .
Почему это важно?
Прежде чем мы сможем сложить или вычесть дроби, дроби должны иметь общий знаменатель
Другими словами, знаменатели должны совпадать с .
Делаем знаменатели одинаковыми
Чтобы сделать знаменатели одинаковыми, мы можем:
Умножьте верхнюю и нижнюю часть каждой дроби на знаменатель другой дроби.
Как в этом примере (нажмите кнопку воспроизведения) :
Это всегда работает, но нам часто нужно впоследствии упростить дробь, как в этом примере (нажмите кнопку воспроизведения) :
Мы упростили дробь 20 32 до 10 16 , затем до 5 8 , разделив верхнюю и нижнюю части на 2 каждый раз, и это очень просто!
Что мы сделали?
1. Мы умножили каждую дробь на знаменатель другой. Давайте использовать буквы вместо цифр:
Мы умножили каждую дробь на знаменатель другой. Давайте использовать буквы вместо цифр:
2. И поскольку теперь у них одинаковый знаменатель, мы можем сложить их:
за один шаг!
Мы можем сделать эти две вещи за один шаг следующим образом:
Что мы используем так:
Пример: Что такое
2 3 + 4 5 ?2 3 + 4 5 = 2 × 5 + 3 × 4 3 × 5 = 10 + 12 15 = 22 15
(Примечание: a было 2, b было 3, c было 4 и d было 5.)
Так делают специалисты!
1698, 1699, 1700, 1701
Общий знаменатель: нахождение и дроби — Видео и стенограмма урока
Наименьший общий знаменатель
Есть два способа найти общий знаменатель для двух или более дробей. Первый метод заключается в нахождении наименьшего общего знаменателя или наименьшего целого числа, которое делится на оба знаменателя.Чтобы найти наименьший общий знаменатель, перечислите кратные каждого знаменателя, а затем выберите наименьший.
Первый метод заключается в нахождении наименьшего общего знаменателя или наименьшего целого числа, которое делится на оба знаменателя.Чтобы найти наименьший общий знаменатель, перечислите кратные каждого знаменателя, а затем выберите наименьший.
Рассмотрим пример:
Сначала мы найдем кратные каждому знаменателю.
Кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.. .
Кратные 7: 7, 14, 21, 28, 35, 42.. .
Наименьшее общее число 3 и 7 — 21. Следовательно, 21 — наименьший общий знаменатель.
Второй метод нахождения общего знаменателя для двух или более дробей — это умножение знаменателей друг на друга.
Рассмотрим другой пример:
Знаменатели 6 и 8. Итак, 6 * 8 = 48; следовательно, общий знаменатель — 48. Хотя этот метод может показаться более простым, общий знаменатель может не быть наименьшим общим знаменателем, а это означает, что в конце задачи сложения или вычитания дробь должна быть уменьшена до самой простой формы.
Сложение дробей
После нахождения общего знаменателя двух или более дробей мы можем использовать эту информацию для сложения или вычитания дробей и решения задачи. Вернемся к нашему первому примеру:
Сначала мы умножим числитель и знаменатель каждой дроби на те же числа. В данном случае 7/7 и 3/3.
Затем мы сложим их вместе.
Не забудьте указать наименьшую форму дроби. В данном случае дробь 13/21 представлена в простейшем виде.
Вычитание дробей
Теперь вернемся ко второму примеру:
Здесь общий знаменатель равен 48. И снова, следующий шаг — умножить числитель и знаменатель каждой дроби на одинаковые числа.В данном случае 8/8 и 6/6.
5/6 * 8/8 = 40/48
3/8 * 6/6 = 18/48
Теперь решаем задачу вычитания.
40/48 — 18/48 = 22/48
Эта дробь должна быть уменьшена путем деления каждого числа на наибольший общий множитель, который в данном случае равен 2:
22/48 сокращается до 11/24 , что и есть наш окончательный ответ.
Пример задачи
Попробуем еще один пример. Найдите общий знаменатель для:
Кратные 2: 2, 4, 6, 8, 10, 12, 14.. .
Кратные 5: 5, 10, 15, 20.. .
Наименьший общий знаменатель равен 10.
В качестве альтернативы мы можем перемножить два знаменателя (2 * 5 = 10), а затем использовать умножение, чтобы получить общие знаменатели дробей:
Наконец, складываем дроби вместе:
Итоги урока
Давайте рассмотрим. Чтобы сложить или вычесть одну дробь (или часть целого) из другой, они должны иметь общий знаменатель или тот же знаменатель. Числитель сообщает нам, сколько частей доступно, а знаменатель описывает, сколько частей находится в целом. Первый метод поиска общего знаменателя заключается в нахождении наименьшего общего знаменателя или наименьшего целого числа, которое делится на оба знаменателя. Второй метод нахождения общего знаменателя для двух или более дробей — это умножение знаменателей друг на друга, в результате чего может потребоваться уменьшение на путем деления каждого числа на наибольший общий множитель.
Числитель сообщает нам, сколько частей доступно, а знаменатель описывает, сколько частей находится в целом. Первый метод поиска общего знаменателя заключается в нахождении наименьшего общего знаменателя или наименьшего целого числа, которое делится на оба знаменателя. Второй метод нахождения общего знаменателя для двух или более дробей — это умножение знаменателей друг на друга, в результате чего может потребоваться уменьшение на путем деления каждого числа на наибольший общий множитель.
— наименьшее общее кратное
Использование калькулятора
Наименьшее общее кратное ( LCM ) также называется наименьшим общим кратным ( LCM ) и наименьшим общим делителем ( LCD) . Для двух целых чисел a и b, обозначенных LCM (a, b), LCM — это наименьшее положительное целое число, которое без остатка делится как на a, так и на b. Например, LCM (2,3) = 6 и LCM (6,10) = 30.
Например, LCM (2,3) = 6 и LCM (6,10) = 30.
НОК двух или более чисел — это наименьшее число, которое делится на все числа в наборе без остатка.
Калькулятор наименьшего общего множественного числа
Найдите НОК набора чисел с помощью этого калькулятора, который также показывает шаги и способы выполнения работы.
Введите числа, для которых нужно найти LCM. Вы можете использовать запятые или пробелы для разделения чисел. Но не используйте запятые в числах.Например, введите 2500, 1000 , а не 2500, 1000 .
Как найти наименьшее общее кратное LCM
Этот калькулятор LCM с шагами находит LCM и показывает работу с использованием 5 различных методов:
- Объявление кратного
- Основная факторизация
- Метод торта / лестницы
- Метод деления
- Использование наибольшего общего множителя GCF
Как найти LCM путем перечисления кратных
- Перечислять кратные каждого числа до тех пор, пока хотя бы одно из кратных не появится во всех списках
- Найдите наименьшее число во всех списках
- Это номер LCM
Пример: LCM (6,7,21)
- Кратное 6: 6, 12, 18, 24, 30, 36, 42 , 48, 54, 60
- Кратное 7: 7, 14, 21, 28, 35, 42 , 56, 63
- , кратное 21: 21, 42 , 63
- Найдите наименьшее число во всех списках.
 Он выделен жирным шрифтом выше.
Он выделен жирным шрифтом выше. - Итак, LCM (6, 7, 21) равно 42
Как найти LCM методом простой факторизации
- Найдите все простые множители каждого заданного числа.
- Перечислите все найденные простые числа столько раз, сколько они встречаются чаще всего для любого данного числа.
- Умножьте список простых множителей вместе, чтобы найти НОК.
LCM (a, b) вычисляется путем нахождения разложения на простые множители как a, так и b.Используйте тот же процесс для НОК более двух чисел.
Например, для LCM (12,30) находим:
- Разложение на простые множители 12 = 2 × 2 × 3
- Разложение на простые множители 30 = 2 × 3 × 5
- Используя все простые числа, которые встречаются так часто, как каждое встречается чаще всего, мы берем 2 × 2 × 3 × 5 = 60
- Следовательно, LCM (12,30) = 60.

Например, для LCM (24,300) находим:
- Разложение на простые множители 24 = 2 × 2 × 2 × 3
- Разложение на простые множители 300 = 2 × 2 × 3 × 5 × 5
- Используя все простые числа, которые встречаются так часто, как каждое встречается чаще всего, мы берем 2 × 2 × 2 × 3 × 5 × 5 = 600
- Следовательно, LCM (24,300) = 600.
Как найти LCM методом простой факторизации с использованием экспонентов
- Найдите все простые множители каждого заданного числа и запишите их в экспоненциальной форме.
- Перечислите все найденные простые числа, используя наивысший показатель степени, найденный для каждого из них.
- Умножьте список простых множителей на показатели вместе, чтобы найти НОК.

Пример: LCM (12,18,30)
- Простые множители 12 = 2 × 2 × 3 = 2 2 × 3 1
- Простые множители 18 = 2 × 3 × 3 = 2 1 × 3 2
- Простые множители 30 = 2 × 3 × 5 = 2 1 × 3 1 × 5 1
- Перечислите все найденные простые числа столько раз, сколько они чаще всего встречаются для любого заданного числа, и умножьте их вместе, чтобы найти НОК.
- 2 × 2 × 3 × 3 × 5 = 180
- Используя вместо этого экспоненты, перемножьте каждое из простых чисел с наибольшей степенью
- Итак, LCM (12,18,30) = 180
Пример: LCM (24,300)
- Простые множители 24 = 2 × 2 × 2 × 3 = 2 3 × 3 1
- Простые множители 300 = 2 × 2 × 3 × 5 × 5 = 2 2 × 3 1 × 5 2
- Перечислите все найденные простые числа столько раз, сколько они чаще всего встречаются для любого заданного числа, и умножьте их вместе, чтобы найти НОК.

- 2 × 2 × 2 × 3 × 5 × 5 = 600
- Используя вместо этого экспоненты, перемножьте каждое из простых чисел с наибольшей степенью
- Итак, LCM (24,300) = 600
Как найти LCM с помощью метода тортов (лестничный метод)
Метод пирога использует деление, чтобы найти НОК набора чисел.Люди используют метод торта или лестницы как самый быстрый и простой способ найти НОК, потому что это простое деление.
Метод тортов такой же, как лестничный метод, блочный метод, факторный блочный метод и сеточный метод ярлыков для поиска НОК. Ящики и сетки могут выглядеть немного иначе, но все они используют деление на простые числа для нахождения НОК.
Найдите LCM (10, 12, 15, 75)
- Запишите свои числа в корж (ряд)
- Разделите номера слоев на простое число, которое без остатка делится на два или более чисел в слое, и перенесите результат на следующий уровень.

- Если какое-либо число в слое не делится без остатка, просто уменьшите это число.
- Продолжайте разделять коржи на простые числа.
- Когда больше нет простых чисел, которые равномерно делятся на два или более чисел, все готово.
- НОК — это произведение чисел в форме буквы L, левом столбце и нижнем ряду.1 игнорируется.
- НОК = 2 × 3 × 5 × 2 × 5
- НОК = 300
- Следовательно, LCM (10, 12, 15, 75) = 300
Как найти НОК методом деления
Найдите LCM (10, 18, 25)
- Запишите свои числа в верхнюю строку таблицы
- Начиная с наименьших простых чисел, разделите строку чисел на простое число, которое без остатка делится хотя бы на одно из ваших чисел, и перенесите результат в следующую строку таблицы.

- Если какое-либо число в строке не делится без остатка, просто уменьшите это число.
- Продолжайте делить строки простыми числами, которые равномерно делятся хотя бы на одно число.
- Когда в последней строке результатов все единицы, все готово.
- НОК — произведение простых чисел в первом столбце.
- НОК = 2 × 3 × 3 × 5 × 5
- НОК = 450
- Следовательно, LCM (10, 18, 25) = 450
Как найти LCM по GCF
Формула для нахождения НОК с использованием наибольшего общего коэффициента GCF набора чисел:
НОК (a, b) = (a × b) / GCF (a, b)
Пример: найти НОК (6,10)
- Найдите GCF (6,10) = 2
- Используйте формулу НОК по ОКФ для вычисления (6 × 10) / 2 = 60/2 = 30
- Итак, LCM (6,10) = 30
Коэффициент — это число, которое получается, когда вы можете равномерно разделить одно число на другое. В этом смысле фактор также известен как делитель.
В этом смысле фактор также известен как делитель.
Наибольший общий делитель двух или более чисел — это наибольшее число, разделяемое всеми множителями.
Наибольший общий множитель GCF такой же, как:
- HCF — наибольший общий множитель
- GCD — Наибольший общий делитель
- HCD — Наивысший общий делитель
- GCM — Величайшая общая мера
- HCM — высшая общая мера
Как найти НОК десятичных чисел
- Найдите число с наибольшим количеством десятичных знаков
- Подсчитайте количество десятичных знаков в этом числе.Назовем этот номер D.
- Для каждого вашего числа переместите десятичную точку D вправо. Все числа станут целыми.
- Найдите НОК набора целых чисел
- Для LCM переместите десятичные разряды D влево.
 Это НОК для исходного набора десятичных чисел.
Это НОК для исходного набора десятичных чисел.
Свойства
LCMНОК ассоциативно:
НОК (а, б) = НОК (б, а)
НОК коммутативен:
НОК (a, b, c) = НОК (НОК (a, b), c) = НОК (a, НОК (b, c))
LCM распределительный:
НОК (da, db, dc) = dLCM (a, b, c)
НОК относится к наибольшему общему коэффициенту (GCF):
НОК (a, b) = a × b / GCF (a, b) и
GCF (a, b) = a × b / LCM (a, b)
Список литературы
[1] Цвиллинджер, Д.(Ред.). Стандартные математические таблицы и формулы CRC, 31-е издание, Нью-Йорк, Нью-Йорк: CRC Press, 2003, стр. 101.
[2] Вайсштейн, Эрик В.
Наименьший общий множитель. Из MathWorld — Интернет-ресурс Wolfram.
Из MathWorld — Интернет-ресурс Wolfram.
— определение, как найти общий знаменатель, примеры, часто задаваемые вопросы
Общий знаменатель помогает выполнять множество математических операций с числами.Важное понятие в математике — сложение и вычитание дробей. Дроби включают числитель (число вверху) и знаменатель (число внизу). Дроби, имеющие одинаковые знаменатели, такие знаменатели называются общими знаменателями. Рассмотрим следующие примеры: 1/2 + 1/2 = 1 и 3/4 + 1/4 = 1 В обоих случаях знаменатели в дробях общие, поэтому легко вычислить ответ.
Однако, если вам задают задачу с разными знаменателями, как бы вы ее решили.Расчет 2/5 + 3/4 затруднен из-за разных знаменателей. Поскольку знаменатели в дробях не совпадают, мы должны решить их другим методом. Давайте исследуем эту тему, чтобы узнать больше об общих знаменателях.
Что такое общий знаменатель?
Две или более дроби, имеющие одинаковый знаменатель, называются общим знаменателем. Общий знаменатель помогает легко выполнять числовые вычисления.Число, показанное в нижней части дроби, называется знаменателем . Знаменатель показывает, на сколько равных частей разделен предмет.
Общий знаменатель помогает легко выполнять числовые вычисления.Число, показанное в нижней части дроби, называется знаменателем . Знаменатель показывает, на сколько равных частей разделен предмет.
На приведенном выше рисунке первая пицца состоит из 4 частей. Таким образом, он представлен как 1, то есть целое. Когда мы убираем один ломтик, у нас остается 3 ломтика из 4. Таким образом, доля оставшихся ломтиков равна 3/4. Это также означает, что убрано 1/4 среза. Если мы сложим эти два, мы получим: 1/4 + 3/4 = 4/4 = 1.Далее, в зависимости от размера пиццы, вы можете разделить ее на любое количество частей.
Как найти общий знаменатель?
Хотя пример с пиццей показывает, насколько просто найти общий знаменатель, такая ситуация может возникнуть не всегда. Иногда вас просят сложить дроби с разными знаменателями, например 3/7 + 12/13. В таких случаях нам нужно найти общий знаменатель, а затем решить дроби.Давайте посмотрим на более простой пример 1/3 + 1/6. Ниже приведены два общих знаменателя методов , чтобы найти ответ:
Ниже приведены два общих знаменателя методов , чтобы найти ответ:
Когда вы решаете общий знаменатель с помощью метода НОК, вы находите наименьшее общее кратное данных чисел. В этом уравнении наименьшее общее кратное равно 6. Следовательно, уравнение принимает вид 1/3 + 1/6 = (1 x 2 + 1) / 6 = (2 + 1) / 6 = 3/6 = 1/2. Если вы перемножите крест, вы найдете решение как: 1/3 + 1/6 = 2/6 + 1/6 = (2 + 1) / 6 = 3/6 = 1/2
Примеры общего знаменателя
Примеры общих знаменателей в нашей повседневной жизни: кусочки пиццы, деньги, приготовление пищи и выпечка и так далее.Например, пицца может быть нарезана на четыре части, а возможные части пиццы могут составлять 1/4. 2/4, 3/4 соответственно. Кроме того, мы можем найти общие знаменатели в тех случаях, когда мы разделяем равные количества количества. В такой ситуации общие знаменатели будут равны 1/2 и 1/2 или 1/4 и 1/4 соответственно.
Практически большинство примеров из повседневной жизни, где количества были разделены, можно выразить как общий знаменатель. Еще один хороший пример общего знаменателя можно найти в кулинарии и выпечке — вам нужны дроби и знаменатели, чтобы измерить ингредиенты для приготовления торта.
Еще один хороший пример общего знаменателя можно найти в кулинарии и выпечке — вам нужны дроби и знаменатели, чтобы измерить ингредиенты для приготовления торта.
Метод общего знаменателя
Методы общего знаменателя, как объяснено выше, включают вычисление наименьшего общего кратного или перекрестное умножение. Общие знаменатели — это произведения знаменателей данных дробей. Однако вы должны помнить, что, помимо этого, общими знаменателями являются также факторы, которые являются общими для дробей, и факторы, которые делают каждую дробь уникальной. Общий знаменатель включает все множители из каждой дроби.
Связанные темы
Ниже перечислены несколько тем, связанных с общим знаменателем, обратите внимание.
Часто задаваемые вопросы по общему знаменателю
Что такое общий знаменатель?
Общий знаменатель — это знаменатель, в котором знаменатель, то есть число под дробью, одинаково во всем, что упрощает процесс вычислений. Если у двух дробей нет общего знаменателя, вам нужно вычислить общий знаменатель, чтобы получить ответ.
Если у двух дробей нет общего знаменателя, вам нужно вычислить общий знаменатель, чтобы получить ответ.
Как найти общий знаменатель?
Для такой суммы, как 3/4 + 1/4 = 1, общий знаменатель равен 4. Однако, когда вам дается расчет, такой как 3/4 + 1/2, вам нужно будет найти общий знаменатель для обоих 3/4 + 1/2. Вы можете сделать это, найдя наименьшее общее кратное или перемножив указанное выше уравнение.
Какой общий знаменатель у 3 и 4?
В отличие от предыдущего примера, в этом случае ни 3, ни 4 не являются множителями друг друга.В этом случае вы можете вычислить значение общего знаменателя, умножив оба числа, чтобы получить 12.
Какое еще название общего знаменателя?
Другое возможное название общего знаменателя — это общий делитель. Далее, исходя из знаменателей, общим знаменателем может быть 1 см двух знаменателей. Кроме того, если один знаменатель является множителем другого знаменателя, то мы можем принять большее число как наименьший общий знаменатель.
Как найти наименьший общий знаменатель?
Наименьший общий знаменатель зависит от вида знаменателя.Для знаменателей с совпадающими простыми числами наименьший общий знаменатель — это произведение двух знаменателей. Кроме того, наименьший общий знаменатель — это 1см двух указанных знаменателей. Давайте рассмотрим два значения знаменателя: 4, 6. Наименьший общий знаменатель — это lcm, равный 4, 6, что является числом 12.
Какой наибольший общий знаменатель?
Наибольший общий знаменатель двух или более дробей, которые не равны нулю, — это наибольшее положительное целое число, которое делит каждый из указанных знаменателей.
Может ли общий знаменатель быть равен нулю или 1?
Для дроби с нулевым общим знаменателем она становится неопределенной. А для дробей, в которых в числителе используются только целые числа, а в знаменателе — 1, общий знаменатель равен 1. В случае, если целые числа рассматриваются как дроби, общий знаменатель равен 1.
Как найти наименьший / наименьший общий знаменатель
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти общую разницу в последовательностях
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Иллюстративная математика
Знаменатели дробей в первой задаче — 5 и 15. 5 делится на 15, а это означает, что 15 делится на 5, поэтому 15 само по себе является общим знаменателем для дробей $ \ frac {1} {5} $ и $ \ frac {1} {15} $. На картинке ниже показано это:
На картинке ниже показано это:
Вот изображение, показывающее дроби, когда они обе записаны в единицах пятнадцатых.
Любое кратное 15 также является общим кратным 5 и 15. Это означает, что $ 2 \ times15 = 30 $ является общим кратным и является общим знаменателем для дробей $ \ frac {1} {5} $ и $ \ frac { 1} {15} $. Таким образом, 15 и 30 — это два разных общих знаменателя для дробей $ \ frac {1} {5} $ и $ \ frac {1} {15} $.
Первый общий знаменатель, который мы определили в части (i), был 15.Вот изображение, представляющее $ \ frac {1} {5} + \ frac {1} {15} $:
Вот как мы можем написать процесс поиска этого общего знаменателя и сложения с помощью символов:
$$ \ begin {align} \ frac {1} {5} + \ frac {1} {15} & = \ frac {1 \ times3} {5 \ times3} + \ frac {1} {15} \\ & = \ frac {3} {15} + \ frac {1} {15} \\ & = \ frac {3 + 1} {15} \\ & = \ frac {4} {15} \ end {align} $$
На рисунке показано, что после преобразования $ \ frac {1} {5} $ в $ \ frac {3} {15} $ мы можем добавить $ \ frac {1} {15} $, и у нас останется $ \ frac { 4} {15} $, как мы обнаружили символически.
Второй общий знаменатель, который мы определили в части (i), равен 30. Вот изображение, которое представляет $ \ frac {1} {5} + \ frac {1} {15} $:
Вот как мы можем написать процесс поиска этого общего знаменателя и сложения с помощью символов:
$$ \ begin {align} \ frac {1} {5} + \ frac {1} {15} & = \ frac {1 \ times6} {5 \ times6} + \ frac {1 \ times2} {15 \ times2} \\ & = \ frac {6} {30} + \ frac {2} {30} \\ & = \ frac {6 + 2} {30} \\ & = \ frac {8} {30} \\ & = \ frac {4 \ times2} {15 \ times2} \\ & = \ frac {4} {15} \\ \ end {align} $$
На рисунке показано, что после преобразования $ \ frac {1} {5} $ в $ \ frac {6} {30} $ и $ \ frac {1} {15} $ в $ \ frac {2} {30} $ мы можем добавить тридцатые и остаться с $ \ frac {8} {30} $.Это решение эквивалентно $ \ frac {4 \ times 2} {15 \ times 2} \ frac {4} {15} $, как мы обнаружили выше. Таким образом, мы получаем тот же ответ, используя два разных общих знаменателя, которые мы определили в части (i), как и следовало ожидать.
Чтобы найти решение проблемы сложения $ \ frac {3} {4} + \ frac {1} {5} $, мы можем сначала найти общий знаменатель. 20 делится на 4 и 5, потому что $ 4 \ times5 = 20 $, что означает, что 20 является общим знаменателем для дробей $ \ frac {3} {4} $ и $ \ frac {1} {5} $.Вот изображение, которое показывает эти дроби, когда они обе записаны в двадцатых числах:
Вот изображение, представляющее $ \ frac {3} {4} + \ frac {1} {5} $:
Вот как мы можем написать процесс поиска общего знаменателя и сложения с помощью символов:
$$ \ begin {align} \ frac {3} {4} + \ frac {1} {5} & = \ frac {3 \ times5} {4 \ times5} + \ frac {1 \ times4} {5 \ times4} \\ & = \ frac {15} {20} + \ frac {4} {20} \\ & = \ frac {15 + 4} {20} \\ & = \ frac {19} {20} \ end {align} $$
На рисунке показано, что когда мы конвертируем $ \ frac {3} {4} $ в $ \ frac {15} {20} $ и $ \ frac {1} {5} $ в $ \ frac {4} {20} $ и прибавив двадцатую, у нас получится $ \ frac {19} {20} $, как мы обнаружили символически.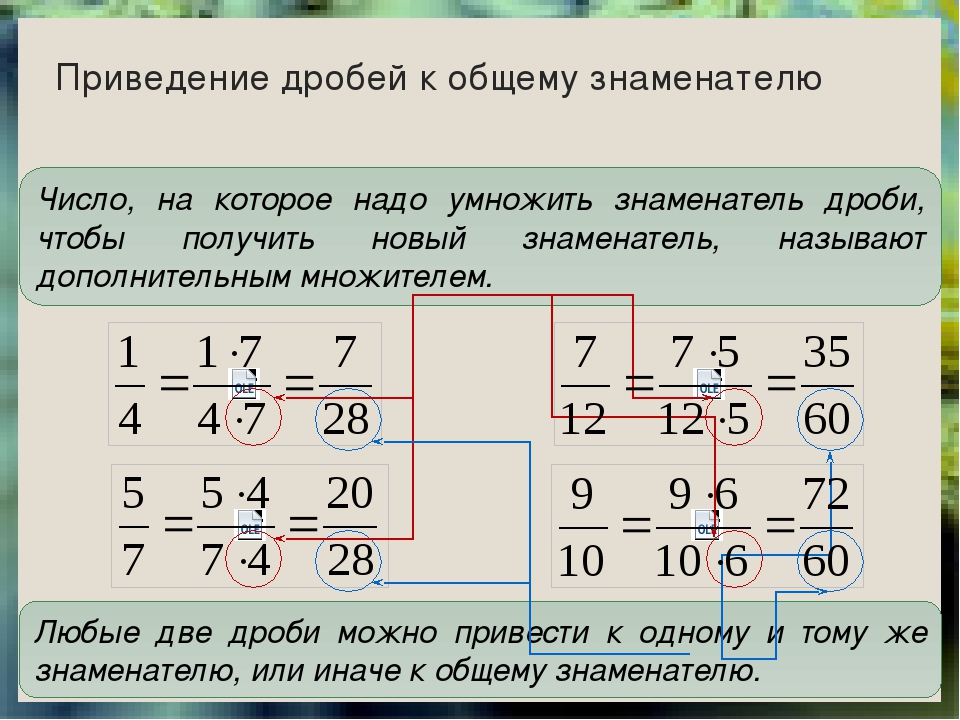
$$ \ begin {align} \ frac {14} {8} + \ frac {5} {12} & = \ frac {14 \ times3} {8 \ times3} + \ frac {5 \ times2} {12 \ times2} \\ & = \ frac {42} {24} + \ frac {10} {24} \\ & = \ frac {52} {24} \ end {align} $$ Если мы остановимся на мгновение, то увидим, что $ \ frac {52} {24} $ эквивалентно $ \ frac {13} {6} $, хотя оба представления суммы верны.



 Не надо постоянно напоминать ему об этом. Особенно если вы знаете, что у вашего ребенка хорошая память. Займитесь своими делами, а его предоставьте самому себе.
Не надо постоянно напоминать ему об этом. Особенно если вы знаете, что у вашего ребенка хорошая память. Займитесь своими делами, а его предоставьте самому себе. Даже не сомневайтесь: скоро эта ваша убежденность перейдет и к нему. А когда подросток уважает себя, он уважает и своих родителей.
Даже не сомневайтесь: скоро эта ваша убежденность перейдет и к нему. А когда подросток уважает себя, он уважает и своих родителей. Он выделен жирным шрифтом выше.
Он выделен жирным шрифтом выше.




 Это НОК для исходного набора десятичных чисел.
Это НОК для исходного набора десятичных чисел.